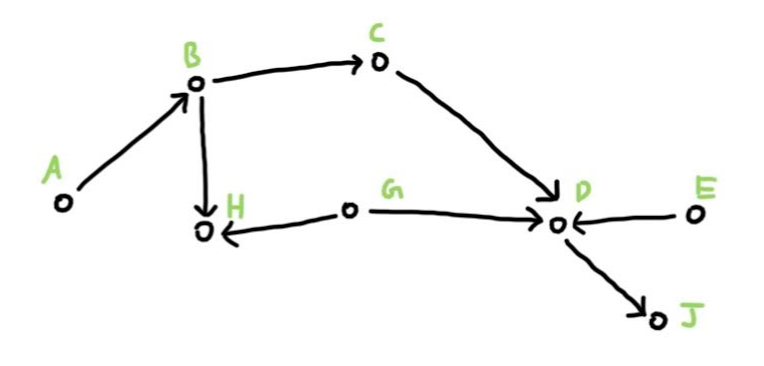
D-Separation

Given the following Bayesian Network, how do you figure out whether A and E are independent or dependent of each other, and what if some nodes are known in the graph, does that change their dependency? D-Separation provides a set of rules to solve just that. Let’s dive in.

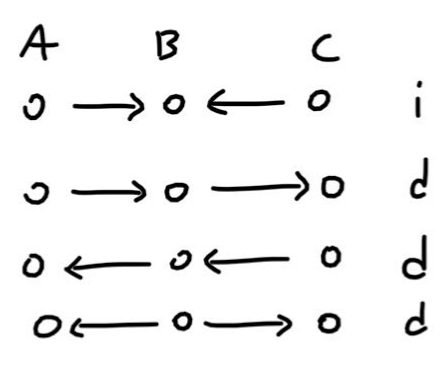
The Different Trios

There are four possible ways three consecutive nodes can be connected in a bayesian network. For each type, we can figure out whether the two outer nodes are independent or dependent. In addition, the middle node could be known or unknown (given / not given). Therefore, we need to look at eight total possibilities. I have listed them below and next to each one I have included i for independent and d for dependent, which indicates whether A and C are independent or dependent of each other. Each case can be proven algebraically. If you are interested in looking at some the math, here is a great set of slides.

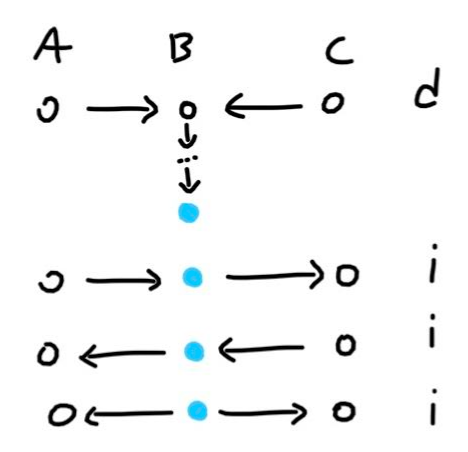
Explaining One Trio

I think the trio that can be the toughest to understand is the first one in the observed category. Let me posit an unrealistic situation. You are hiking on a trail, and at the start of the trail, the trail sign has the following image.

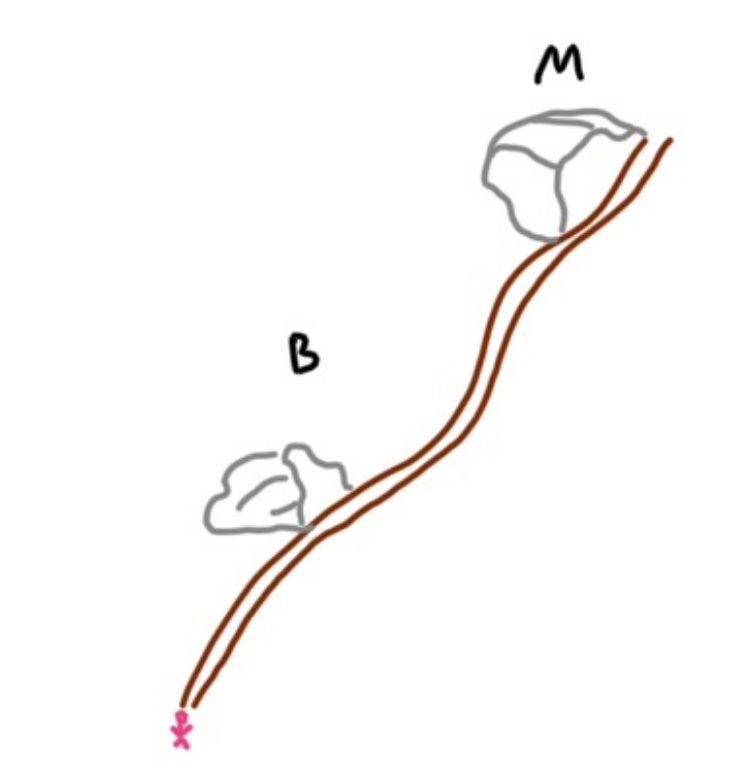
There are two caves on the trail, the first is a bat cave, and the second is a moose cave. Mooses can be dangerous, so on the trail sign, the rangers have posted the following bayesian network.

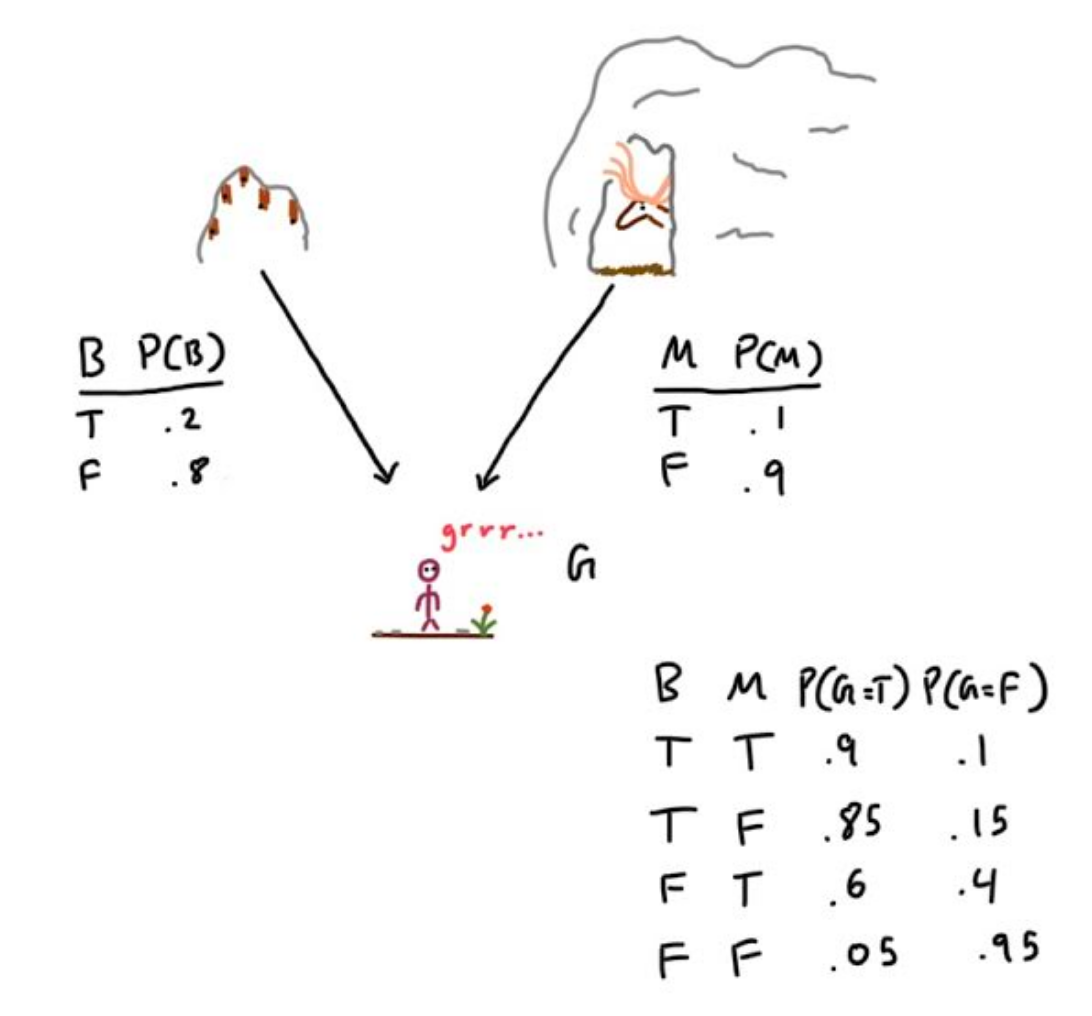
The network tells us the probability of bats being in their cave, and the moose being in its cave. Furthermore, both animals can growl when in their respective caves. Hearing a growl therefore conveys some information about the state of both caves if they haven’t been observed yet. While the sign should probably say don’t hike on this trail, the statistician daredevil still enters the trail, and immediately hears a growl. Upon hearing this growl, they whip out their notebook and calculate the probability that the moose is in the cave given that we heard a growl: P(M = T | G = T).

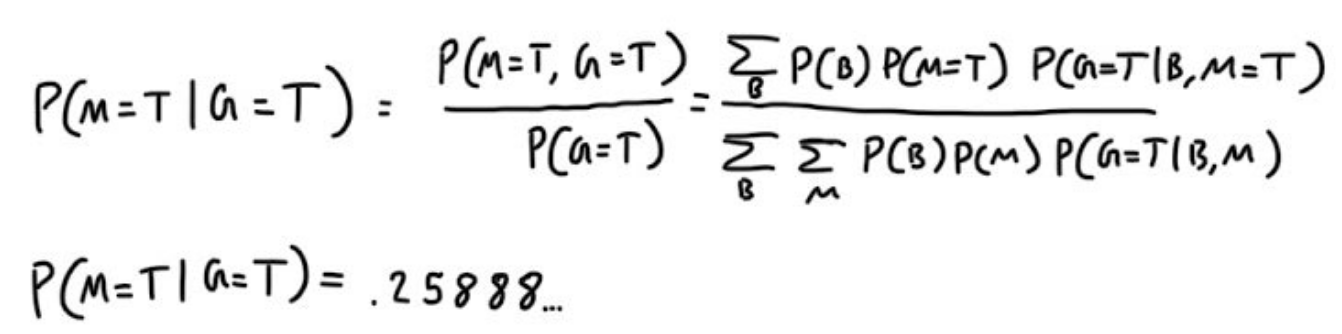
Our probability of the moose residing in the cave, goes up. Does this mean they should turn around? Our clever statistician knows that hiking to the bat cave and observing the bat cave can update the probability of the moose residing in the cave. Therefore, they climb up to the bat cave, and peek inside, and they are joyous to find bats inside. Why are they happy about this? Let’s take a look at what our statistician calculated.

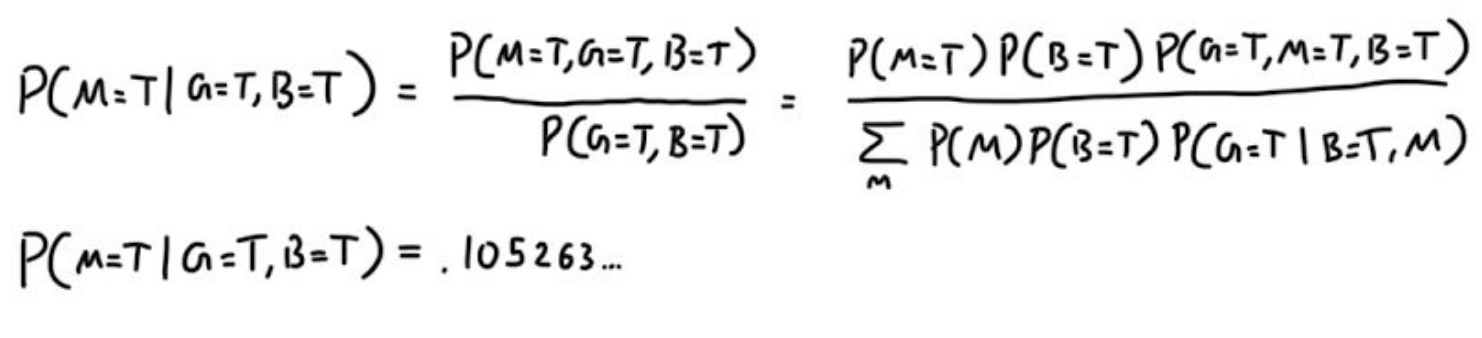
Therefore, the probability of the moose being in the cave went down! Ultimately, We have shown that both B and M are dependent on each other when G is observed.

How To Use The Trios

Let’s use the initial Bayesian Network and make some nodes observed (teal), and we want to know whether the nodes A and E are independent or dependent of each other. Here is our updated graph.

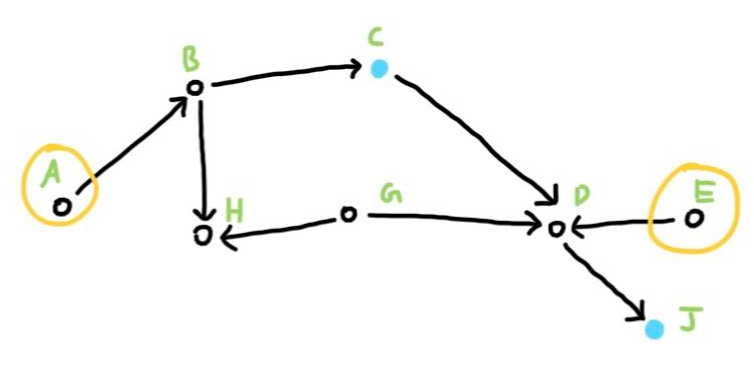
What D-Separation does is look at all paths from A to E. For each path, you need to keep looking at the consecutive three nodes and see if they are independent or dependent. If there is an independent trio, then A and E can’t be dependent via that path. If all paths have an independent trio, then A and E are independent. Think of the dependent trios as walkable paths, where the nodes are dependent and linked. However, in an independent trio, both ends are independent so it’s impossible for the nodes on either end of a path with an independent trio to be dependent/linked. In our example, there are only two paths from A to E. Therefore, we need to observe each path. Here is the first path.

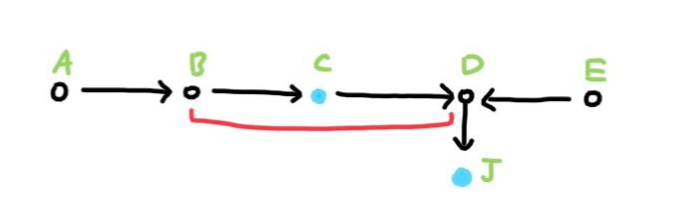
In this path, there is an independent trio (red underline). Thus this path can’t make A and E dependent. On to our next path.

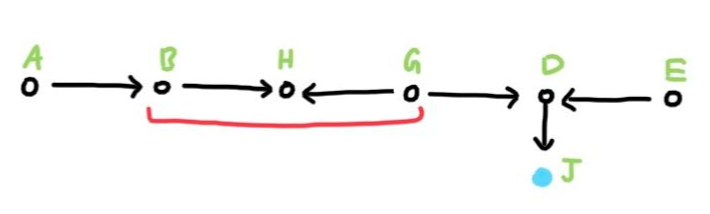
Again, we found another independent trio, which means there exists no path in which A and E can be causally linked / dependent. Thus, A and E are independent of each other.

References

https://ermongroup.github.io/cs228-notes/representation/directed/