Locality Sensitive Hashing for Nearest Neighbor Approximation

For my research, I have to use KNN to obtain the closest set of points for a given point. While calculating the distance between the given point and all other points is guaranteed to provide the closest points, it is slow. For my research, I need the nearest neighbor search to be as fast as possible without compromising the neighbor set too much. Locality Sensitive Hashing (LSH) is a technique that can solve this problem.

How does it work?

If we have a set of points of dimension n, LSH discretizes space. By discretizing the space, we create a function . But the range of this function is finite.

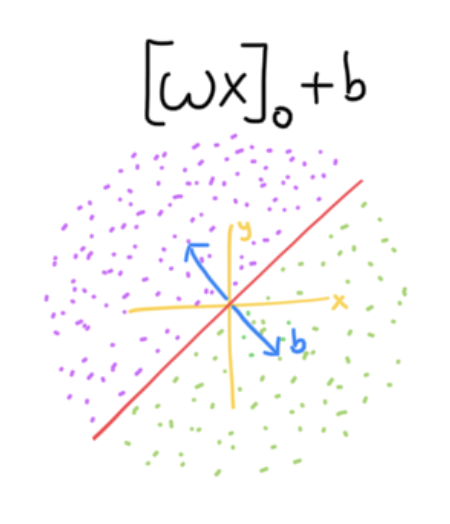
To achieve this we need to create hyperplanes. Since we are in 2D, we need to create lines. These hyperplanes / lines (for 2D) are boundaries. Points on one side are considered distinct from points on the other side. To mathematically create this, we utilize linear algebra. To know which side a point is on with respect to a boundary, we transform all of space including the boundary, such that x = 0. Points after the transformation whose x coordinate are < 0 are on a different side than points whose x coordinate are > 0. To visually see this consider the following diagram.

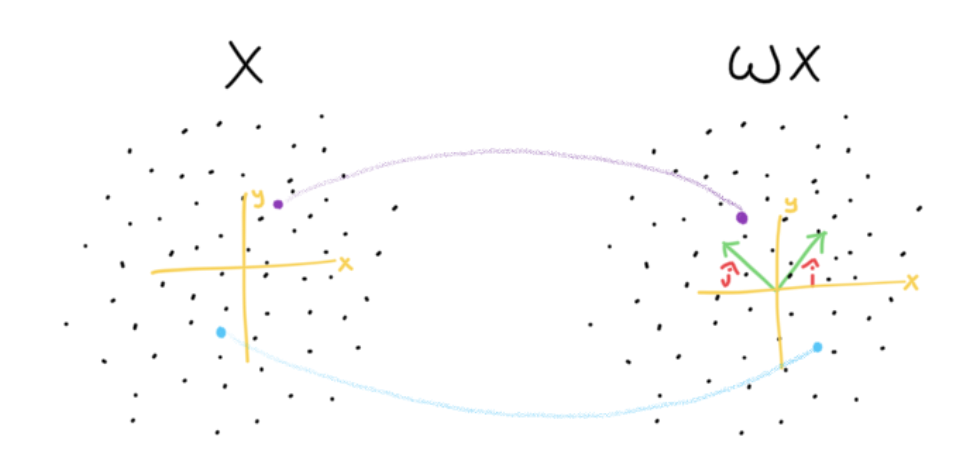
This assumes my projection matrix W is a rotation matrix, rotating the space by 45 degrees counterclockwise, but W can be any random matrix. To figure out which sides of the boundary created by the projection matrix, we can apply the transformation and observe the x coordinate. Thus, this transformation effectively creates the following red boundary line.

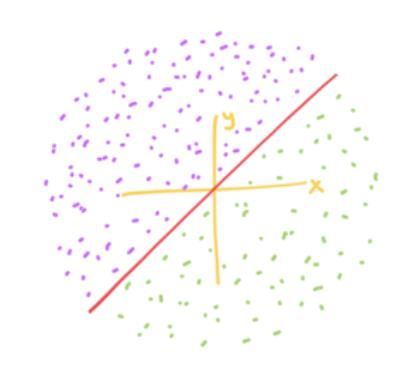
A coded version produces the following:

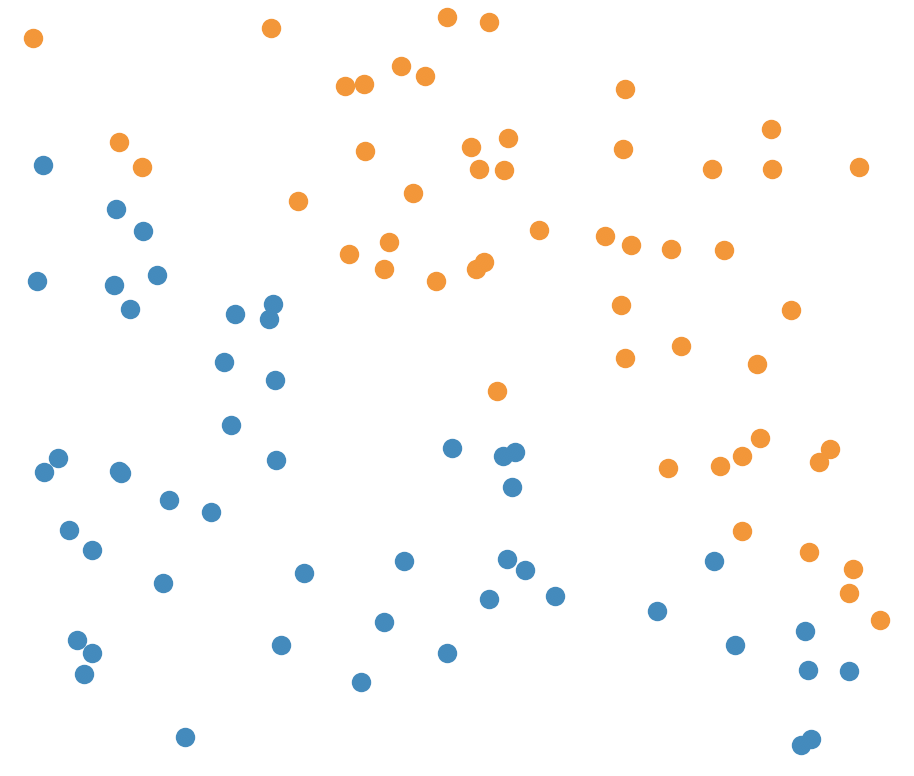
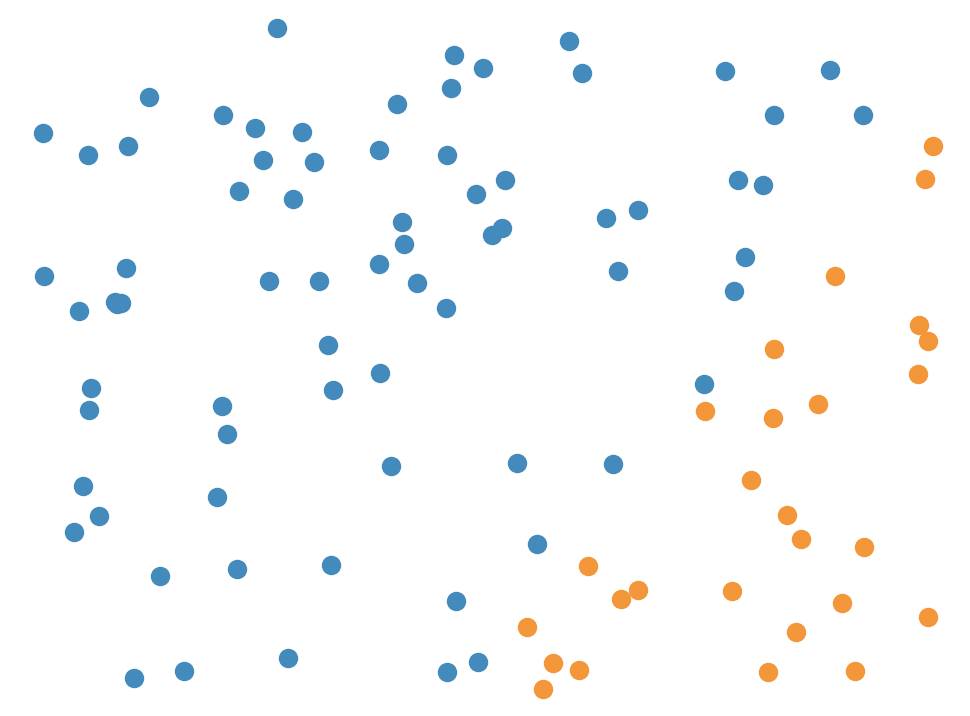
However, there still is an issue with this. If we create many boundary lines, they all will cross the origin. This is bad because …

Clearly we aren’t discretizing the space in an accurate manner. Logically we need to make these boundary lines more “random”, where they don’t have to cross the origin. To achieve this, we need to shift the boundary line after the transformation. Thus we obtain the following equation.

A coded version produces the following:

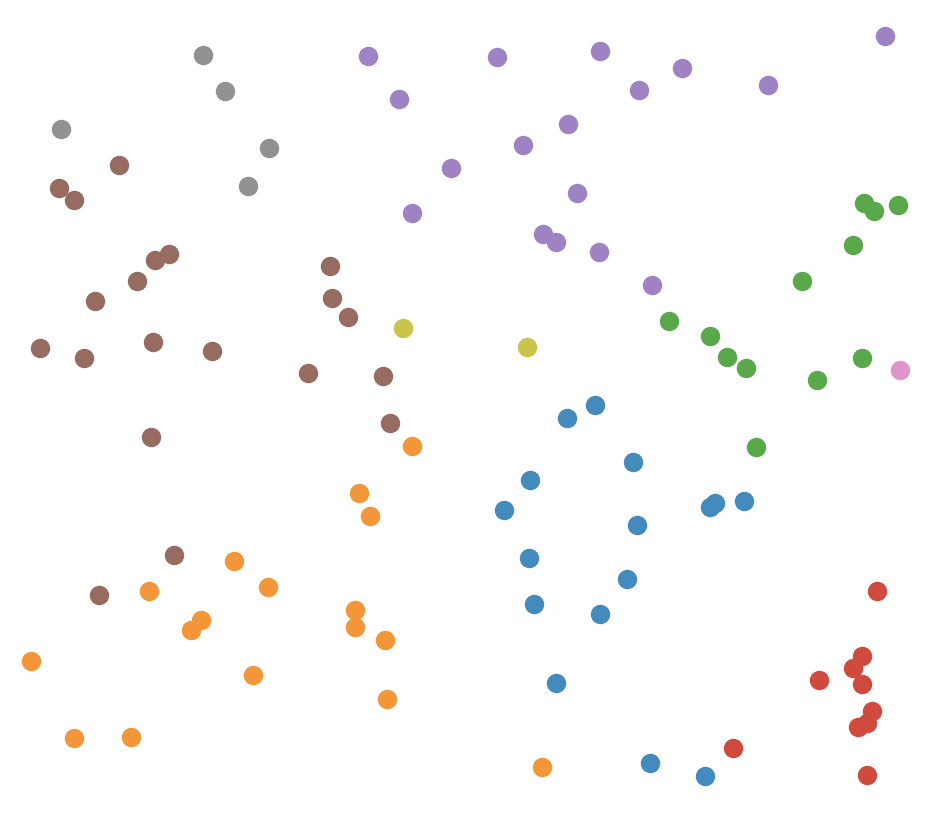
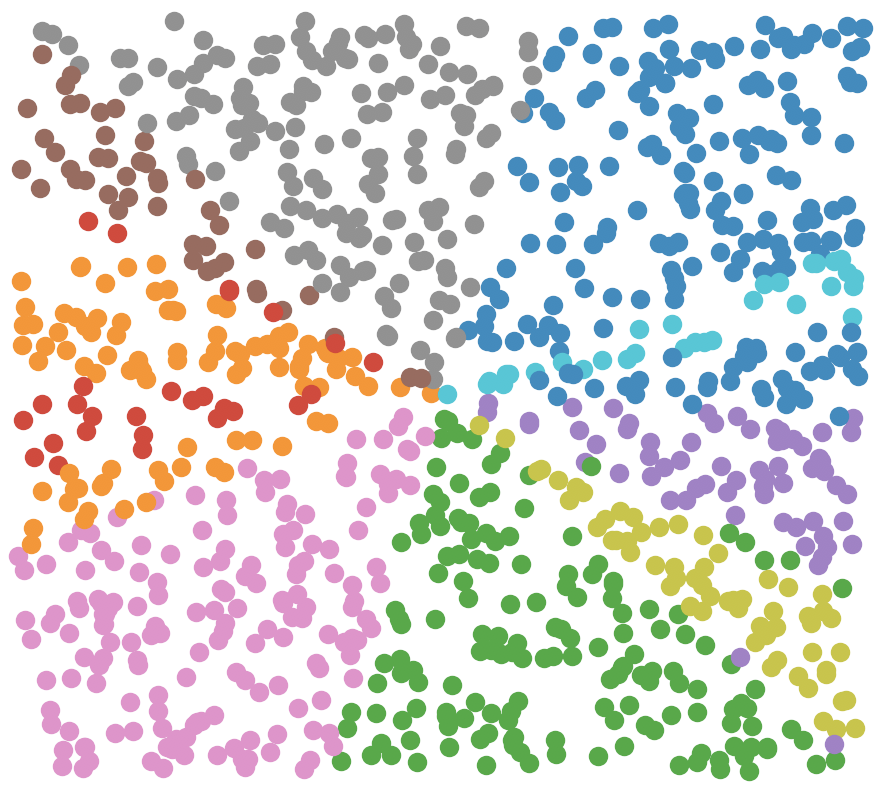
Creating many divisions produces the following diagram:

The current process takes O(dn + (num points in bucket)d) where d is the number of dimensions for each vector and n is the number of boundary hyper planes. This approximately comes to O(dlog(N)) where N is the total number of points. The log should make sense because the number of buckets grows exponentially as the number of boundaries increases.

Why we don’t uniformly chop space

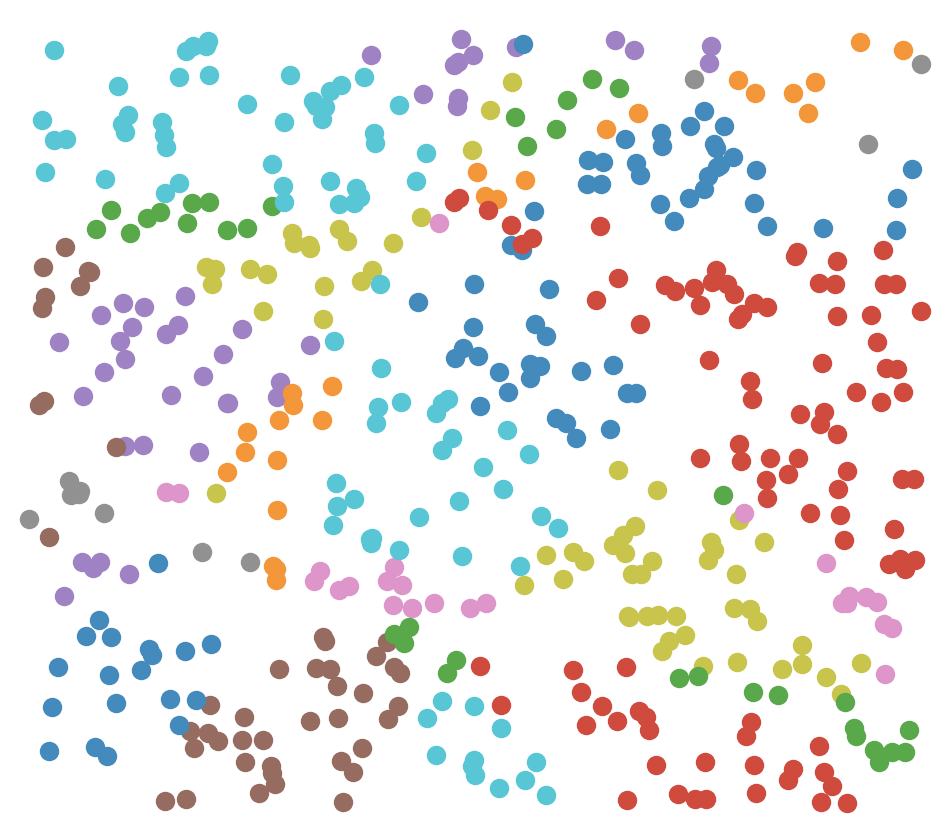
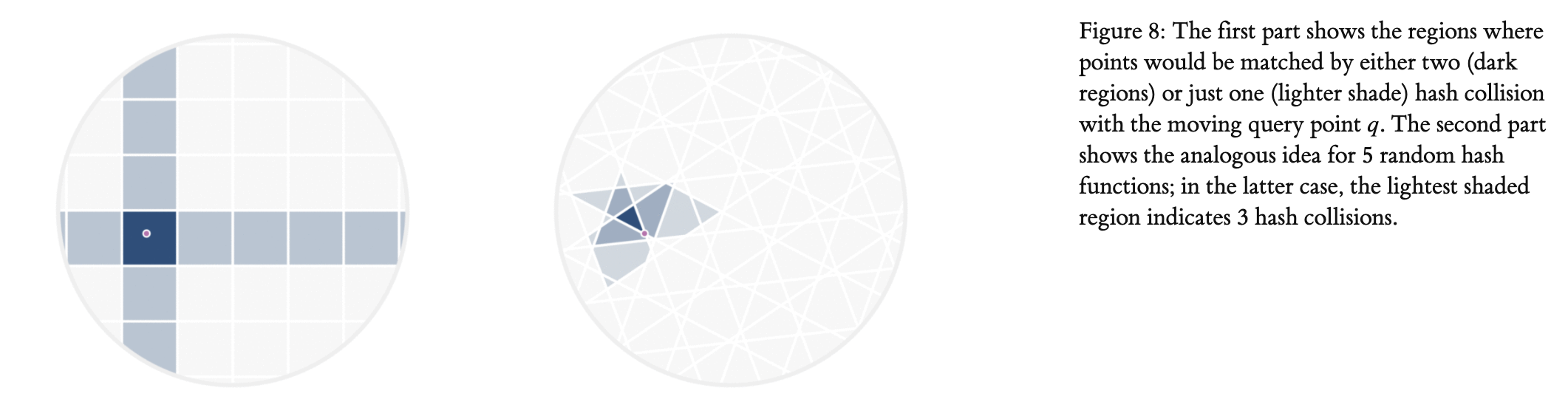
Why go through all the hassle of creating random hyperplanes when we can just make them uniformly spaced like a grid in 2D. Well if we are just searching within a bucket, uniform or non-uniform doesn’t matter much. But if we search outside the grid, then it will matter a lot more. We search outside the grid if we want to go through more points, which will increase accuracy but at the cost of time. To search outside the grid we need to compare hamming distances between buckets. For example, 1 means the point is on one side of a boundary, and 0 is the other side. So if we have 5 boundaries, a point’s bucket is defined as the list of 1’s and 0’s like : [1,0,1,0,0]. If another point’s bucket list is : [0,0,1,0,0] then both points are in neighboring buckets because their hamming distance is 1, which just means that both points’ lists differ by one value (or one boundary). Increasing how far we are willing to search is determined by the hamming distance threshold, the higher it is the further out we can search. With this in mind the following figure from this awesome article should answer the question of why we don’t use uniform hyperplanes.

Code

import matplotlib.pyplot as plt
import numpy as np
from collections import defaultdict

numPts = 500
numBuckets = 15 #total buckets - 1

points = np.random.rand(numPts,2)-.5

projections = np.random.rand(numBuckets,2,2)-.5
shifts = np.random.rand(numBuckets,1)*.5-.25

d = defaultdict(list) #stores the points per bucket
buckets = [] #stores the buckets that have points in them 

for pt in range(points.shape[0]):
	l = []
	for i in range(shifts.shape[0]):
		if((projections[i].dot(points[pt].T))[0] + shifts[i] >= 0):
			l.append(1)
		else:
			l.append(0)
	d[tuple(l)].append((points[pt][0],points[pt][1]))

	if((l in buckets) == False):
		buckets.append(l)

for bucket in buckets: # go through each bucket
	plt.scatter(*zip(*d[tuple(bucket)]))

plt.show()

References

https://www.youtube.com/watch?v=LqcwaW2YE_c
http://tylerneylon.com/a/lsh1/