Monte Carlo Tree Search (MCTS)
In the game of chess, “after both players move, 400 possible board setups exist. After the second pair of turns, there are 197,742 possible games, and after three moves, 121 million. At every turn, players chart a progressively more distinctive path, and each game evolves into one that has probably never been played before.” - Popsci
Based on that, no computer can simulate all possible states and actions in complex games like Chess or Go. Well known techniques such as minimax, can’t work because it requires the whole tree to be exhausted. This is where Monte Carlo Tree Search comes in.
How Does It Work?
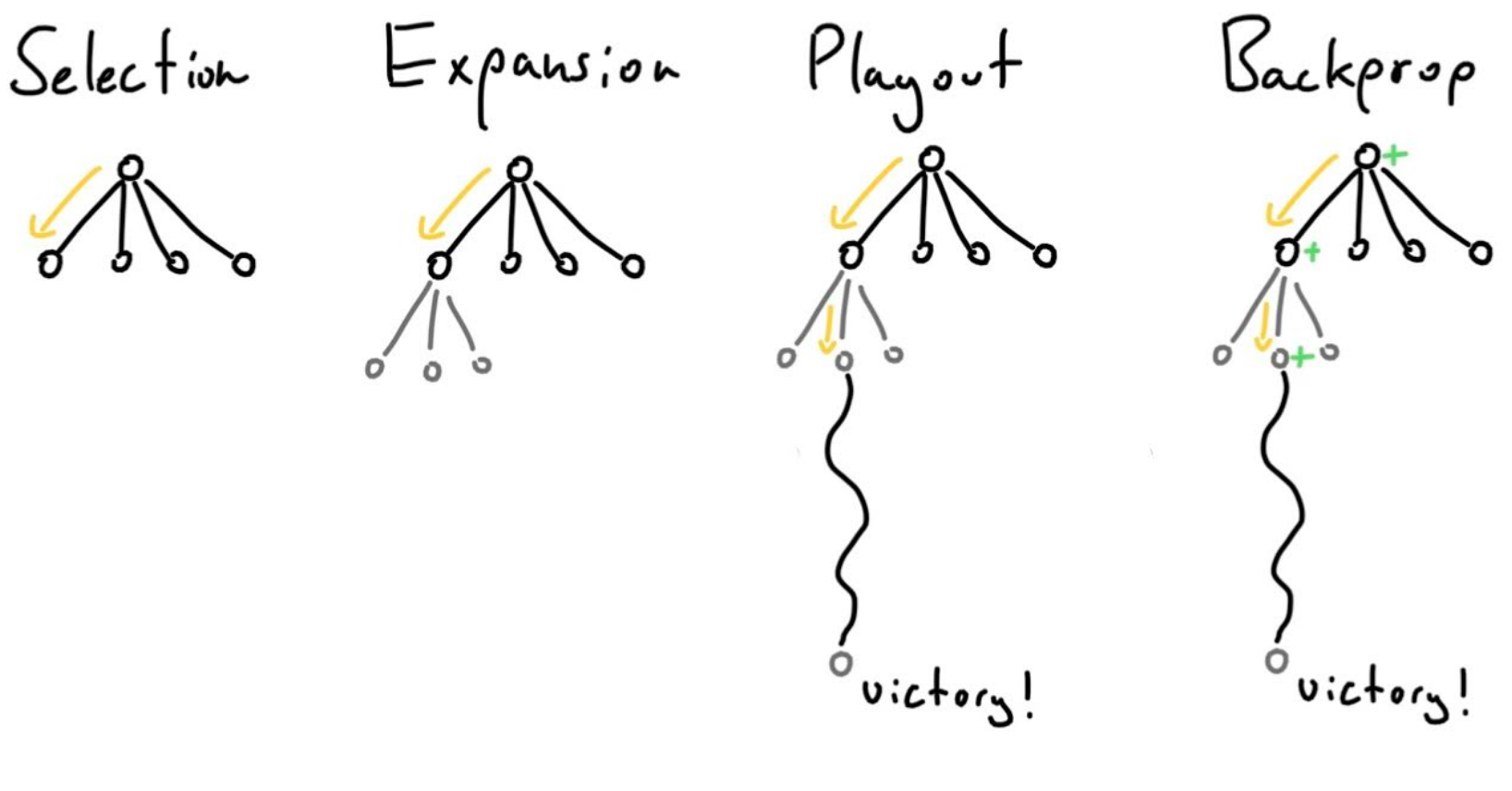
The image above shows the 4 steps that MCTS repeats. Selection traverses the tree by repeatedly choosing the node with the highest UCT value (I’ll define that later). It does that until it hits a leaf node or terminal node. If it reaches a leaf node, it creates nodes for all the possible actions or just one depending on how you want to implement it. Then randomly chose one of the newly created nodes, and run a playout. A playout is just randomly taking actions from a given node until you reach a terminal node. Once the terminal node is reached, you perform backpropagation. Depending on whether the terminal node was a win or not, backpropagation updates the values of the nodes in the path it took to reach that terminal node.
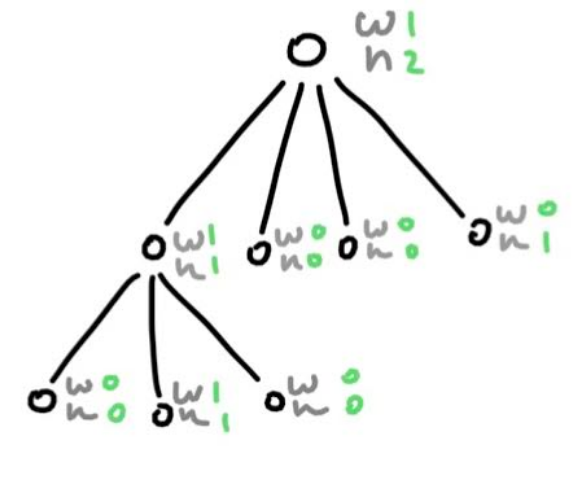
Each node stores two values, one is the number of wins from that node, the other is the number of times the node has been visited. Here is what the node’s values could look like for the tree in the selection step.
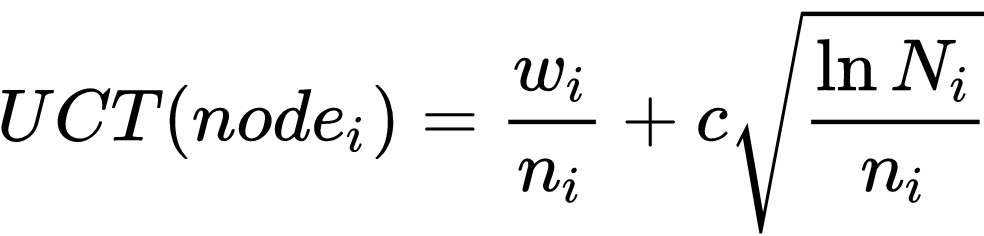
The equation above is the UCT formula. w is the number of wins for the node, n is the number of times that node has been visited, N is the number of times the parent node has been visited. c is a hyperparameter, which is usually set to sqrt(2). So what is the nature of this formula? Since the node with the highest UCT value, we need to figure out what makes the UCT value go up.
Exploration vs Exploitation
Looking at the left term, w/n, if the node is a good one, then that ratio is going to go up. However, the right term is what drives exploration. If a node is not being visited for a while, and its sibling is that the ratio N/n is going to go up. However, MCTS weights this exploration factor not as great as the win to visit ratio since the exploration term is under a square root. Imagine we keep repeating the same aforementioned 4 step process, but our UCT formula did not have the exploration term. Then at every selection process, the node with the highest win ratio would be chosen, and the tree would just grow one long root. The image below describes this.
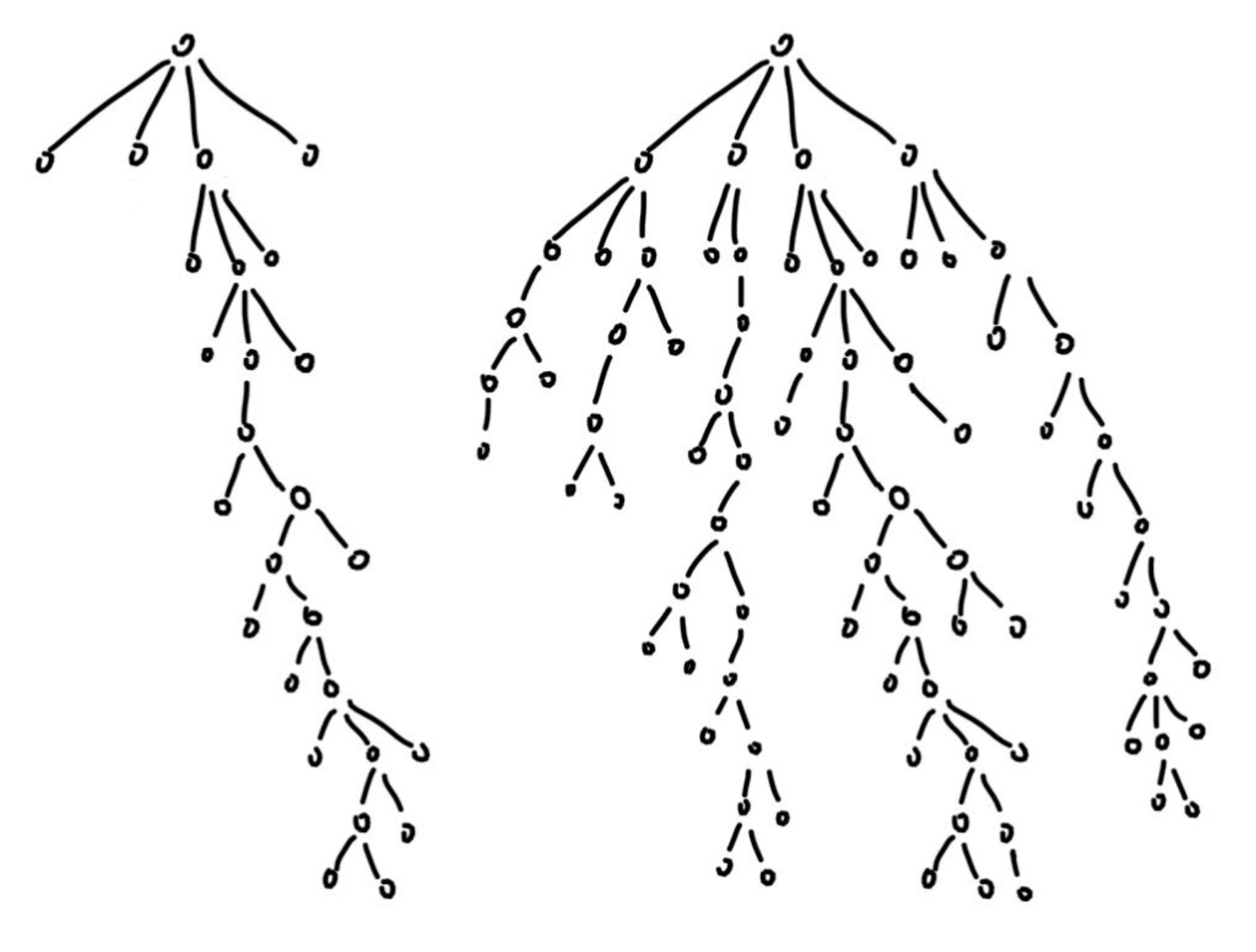
The tree on the left is what could happen if there isn’t an exploration term, and the tree on the right is what is more likely to occur. I assumed that the long root in the left image is a very good path, which is why the tree on the right also focuses it, but it also branches out occasionally in hope of there being other good paths.
Two-Player?
In my implementation I made MCTS learn a 2 player game. How can we adapt our technique then? Well, it is quite straight forward, as this answer puts, we need to treat each layer as player 1 or player 2’s move. The image below describes this.
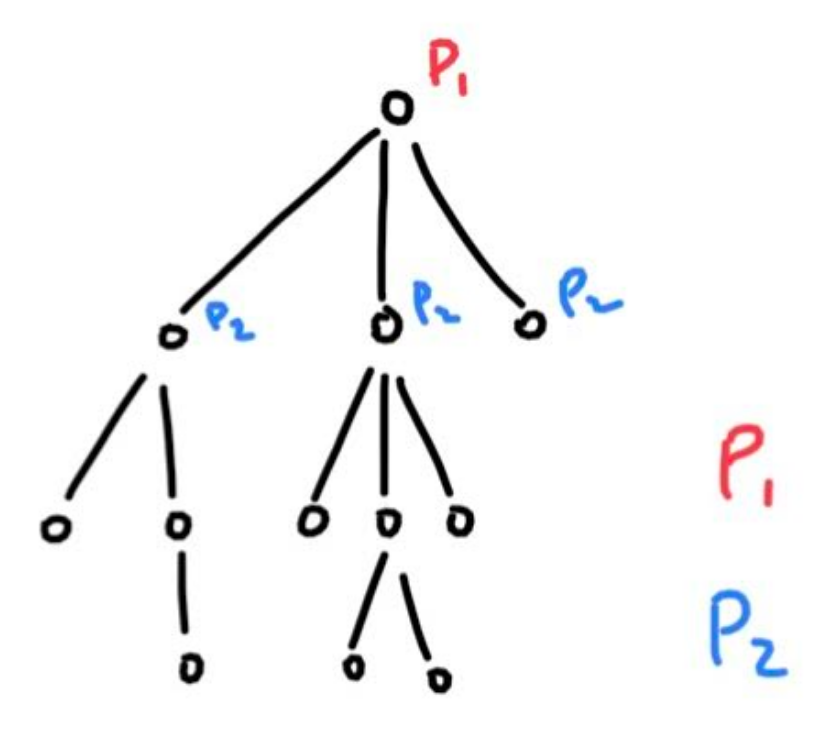
We set the root node as Player 1’s node, so it chooses which action to take from there, and therefore whatever action it takes lands us to the next layer of the tree where the ball is on Player 2’s court, and this keeps repeating. So when we do reach a terminal node, how do we modify our backpropagation? Let’s take a look a the image below to understand.
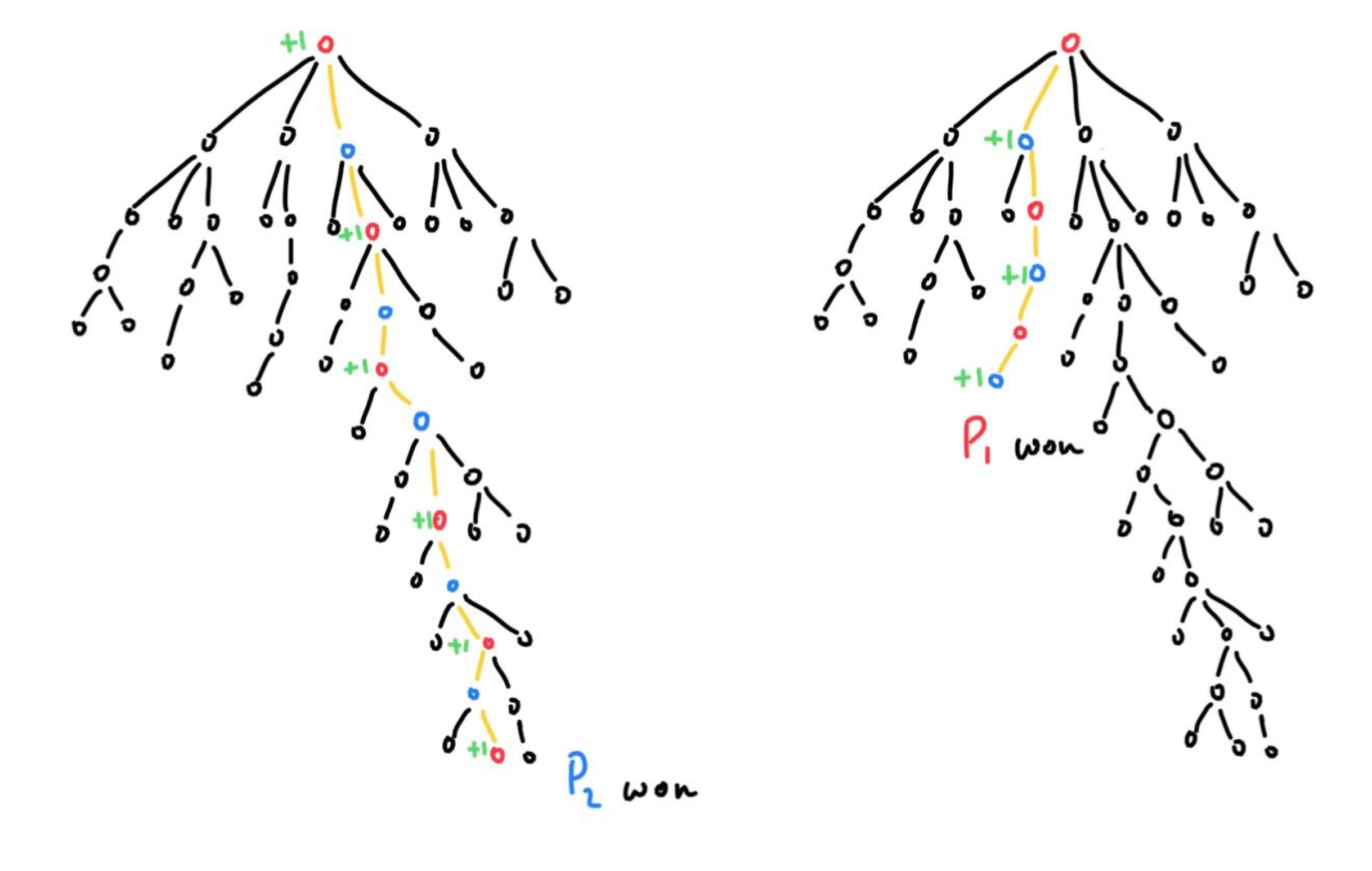
All we have to do is alternate which nodes’ win should be incremented. If Player 1 wins, then starting from the second node in the winning path, every other node’s win will be incremented. If Player 2 wins, its the same, except the starting node is root.
Implementation
Connect 4 is a fun game, which is why we are going to implement a Connect 3 bot. I shrunk the game, so the board is 5x5 and you need 3 pieces in a row or column or diagonal to win. I shrunk the game because it’s faster to run, and implementing the original specs would take a lot more time to run due to exponential branching.
First I need to create a Board class, this handles all the placement of piece and figuring out if there is a winner/draw and for which player. I then needed a Node class, which stores the w,n,children. Finally, I wrote the main file which performs the selection, expansion, playout, and backpropagation. When playing the game once MCTS finished running for 5 million iterations, the computer chose moves based on which child has the most number of wins. Why didn’t I just chose the node with the highest UCT value, well when actually playing I don’t want the computer to be exploring, it in the exploitation mindset :)
Games
Here are couple games where the comptuter (1) made the first move.


Here is a game where I made the first move.

From the first two games, you can see how it learns to 100% checkmate, so when I played the first move, the computer didn’t bother blocking me by placing its piece (2) on the middle column, and instead it placed it on the last column, since regardless, it would always loose from that position.
Where To Go From Hhere?
I only wrote a mini connect 4 game, and I couldn’t use solely MCTS to play the full game (Connect 4) without having to run many many more iterations. There is a solution to this. Use MCTS to traverse the tree normally, but have a neural network watching and learning the moves. For example, you could use QLearning. Using neural networks with MCTS is a powerful combination. This is how AlphaGo got so good. Read this article to better understand how to attach a neural network to MCTS. That’s all for now, thanks for reading!
Code
Board class
import numpy as np
class Board:
def __init__(self,size, winSize):
self.winSize = winSize
self.player = 1
self.size = size
self.board = np.zeros(([self.size,self.size]))
def win(self):
for y in range(self.size): #row
for x in range(self.size - self.winSize + 1):
if(self.row(y,x) == True):
if(self.board[y][x] == 1):
return(1)
else:
return(-1)
for y in range(self.size - self.winSize + 1): #column
for x in range(self.size):
if(self.column(y,x) == True):
if(self.board[y][x] == 1):
return(1)
else:
return(-1)
for y in range(self.size - self.winSize + 1): #diag1
for x in range(self.size - self.winSize + 1):
if(self.diag1(y,x) == True):
if(self.board[y][x] == 1):
return(1)
else:
return(-1)
for y in range(self.size - self.winSize + 1): #diag2
for x in range(self.size - self.winSize, self.size):
if(self.diag2(y,x) == True):
if(self.board[y][x] == 1):
return(1)
else:
return(-1)
return(False) ##no win or draw
def row(self,y,x):
if(self.board[y][x] == 0):
return(False)
for i in range(self.winSize-1):
if(self.board[y][x+1] != self.board[y][x]):
return(False)
x += 1
return(True)
def column(self,y,x):
if(self.board[y][x] == 0):
return(False)
for i in range(self.winSize-1):
if(self.board[y+1][x] != self.board[y][x]):
return(False)
y += 1
return(True)
def diag1(self,y,x):
if(self.board[y][x] == 0):
return(False)
for i in range(self.winSize-1):
if(self.board[y+1][x+1] != self.board[y][x]):
return(False)
x += 1
y += 1
return(True)
def diag2(self,y,x):
if(self.board[y][x] == 0):
return(False)
for i in range(self.winSize-1):
if(self.board[y+1][x-1] != self.board[y][x]):
return(False)
x -= 1
y += 1
return(True)
def move(self, pos):
depth = 0
while(depth+1 < self.size and self.board[depth+1][pos] == 0):
depth += 1
self.board[depth][pos] = self.player
if(self.player == 1):
self.player = 2
else:
self.player = 1
if(len(self.availableMoves()) == 0):
if(self.win() == False):
return(0)
else:
return(self.win())
def undo(self, pos):
depth = 0
while(depth+1 < self.size and self.board[depth][pos] == 0):
depth += 1
self.board[depth][pos] = 0
if(self.player == 1):
self.player = 2
else:
self.player = 1
def reset(self):
self.board = np.zeros(([self.size,self.size]))
self.player = 1
def availableMoves(self):
moves = []
for pos in range(self.size):
if(self.board[0][pos] == 0):
moves.append(pos)
return(moves)
def boardState(self):
return(self.board)
Node class
class Node:
def __init__(self, size, terminal, result):
self.n = 0
self.w = 0
self.terminal = terminal
self.children = [-2 for _ in range(size)]
self.reward = result
main
import numpy as np
from Board import Board
from Node import Node
import math
import random
def uct(node, parentNode):
if(node.n == 0):
return(float("inf"))
return((float(node.w)/node.n) + math.sqrt(2)*math.sqrt((np.log(parentNode.n))/node.n))
def selection(node, l):
l.append(node)
if(node.children == [-2 for _ in range(size)] or node.terminal == True):
return(node.terminal, node)
first = False
maxChild = 0
maxMove = 0
for child in range(len(node.children)):
if(node.children[child] != -2):
uctVal = uct(node.children[child],node)
if(first == False):
maxVal = uctVal
maxChild = node.children[child]
maxMove = child
first = True
if(uctVal > maxVal):
maxVal = uctVal
maxChild = node.children[child]
maxMove = child
board.move(maxMove)
return(selection(maxChild,l))
def play(node):
result = board.move(random.choice(board.availableMoves()))
while(isinstance(result,bool)):
result = board.move(random.choice(board.availableMoves()))
return(result)
def expansion(node):
for move in board.availableMoves():
result = board.move(move)
if(isinstance(result,bool)):
node.children[move] = Node(size, False, 0)
else:
node.children[move] = Node(size, True, result)
board.undo(move)
def backprop(l, res):
for node in range(len(l)):
if(res == -1):
if(node%2 == 0):
l[node].w += 1
if(res == 1):
if(node%2 == 1):
l[node].w += 1
l[node].n += 1
def bestMove(node):
first = False
maxChild = 0
maxMove = 0
for child in range(len(node.children)):
if(node.children[child] != -2):
val = node.children[child].w
if(first == False):
maxVal = val
maxChild = node.children[child]
maxMove = child
first = True
if(val > maxVal):
maxVal = val
maxChild = node.children[child]
maxMove = child
return(maxMove)
size = 5
board = Board(size,3)
root = Node(size, False, 0)
expansion(root)
for i in range(5000000):
if(i%100000 == 0):
print(i)
l = []
res = selection(root, l)
if(res[0] == True):
backprop(l, res[1].reward)
else:
expansion(res[1])
backprop(l,play(res[1]))
board.reset()
Playing
#computer starts
board.reset()
curr = root
while(True):
move = bestMove(curr)
curr = curr.children[move]
board.move(move)
print(board.boardState())
playerMove = int(input())
board.move(playerMove)
curr = curr.children[playerMove]
#player starts
board.reset()
curr = root
while(True):
print(board.boardState())
playerMove = int(input())
board.move(playerMove)
curr = curr.children[playerMove]
move = bestMove(curr)
curr = curr.children[move]
board.move(move)
References
https://en.wikipedia.org/wiki/Minimax
https://en.wikipedia.org/wiki/Monte_Carlo_tree_search