Symmetries in Neural Networks

Intro

I read some cool papers this past few days that convey how to incorporate neural networks symmetries into optimizations or functions that operate on their weights.

Here are the papers:

Improving Convergence and Generalization Using Parameter Symmetries

In many neural networks, different values of the parameters may result in the same loss value. Parameter space symmetries are loss-invariant transformations that change the model parameters....

https://arxiv.org/abs/2305.13404

Symmetry Teleportation for Accelerated Optimization

Existing gradient-based optimization methods update parameters locally, in a direction that minimizes the loss function. We study a different approach, symmetry teleportation, that allows...

https://arxiv.org/abs/2205.10637

Universal Neural Functionals

A challenging problem in many modern machine learning tasks is to process weight-space features, i.e., to transform or extract information from the weights and gradients of a neural network....

https://arxiv.org/abs/2402.05232

Permutation Equivariant Neural Functionals

This work studies the design of neural networks that can process the weights or gradients of other neural networks, which we refer to as neural functional networks (NFNs). Despite a wide range of...

https://arxiv.org/abs/2302.14040

So in this post I am going to mainly focus on the first two optimization papers. The premise is we have a function parameterized by $\theta$ .

\hat{y} = F(x;\theta)

The core idea behind these papers is realizing that depending on the network there might be some symmetries in $\theta$ . What do I mean by symmetries? Well what if I can manipulate $\theta$ without changing the output of $F$ . Let me show you a concrete example to illustrate this. Let’s take a network with just one hidden layer and ignore the bias term for now, and the activation is point wise non-linear, like ReLU.

\hat{y} = W_2 \sigma (W_1x)

I can create a group $G$ of permutations, where $g \in G$ is a permutation that swaps rows of $W_1$ and the columns of $W_2$ . Note the below equation is just one way a group can interact with the weights, one could find more Groups.

\hat{y} = W_2g^{-1}\sigma (gW_1x)

Therefore, a different approach to optimization this network which is illustrated in Bo’s latest paper is to also search for $g$ . So to formalize this, let $W = (W_2, W_1)$ be all the parameters of the network. This just doesn’t apply to the two layer example, and it can apply to any network, but we will use the two layer one for simplicity. You need to find a group $G$ does operates on the weights without changing the function output, in the two layer case it could look like $G = GL(\mathbb{R})$

W_2g^{-1}\sigma (gW_1x) = W_2 \sigma (W_1x), \forall g \in G, \forall W_1, W_2 \in \mathbb{R}^{n \times n}

Then we want to find a $g \in G$ s.t.

g^t = \argmax_{g \in G} || \nabla_WL(g\cdot W^t)||^2

Then we can do vanilla gradient descent on a batch of data $\xi^t$

W^{t+1} = g^t \cdot W^t - \eta \nabla_W L(g^t \cdot W^t, \xi^t)

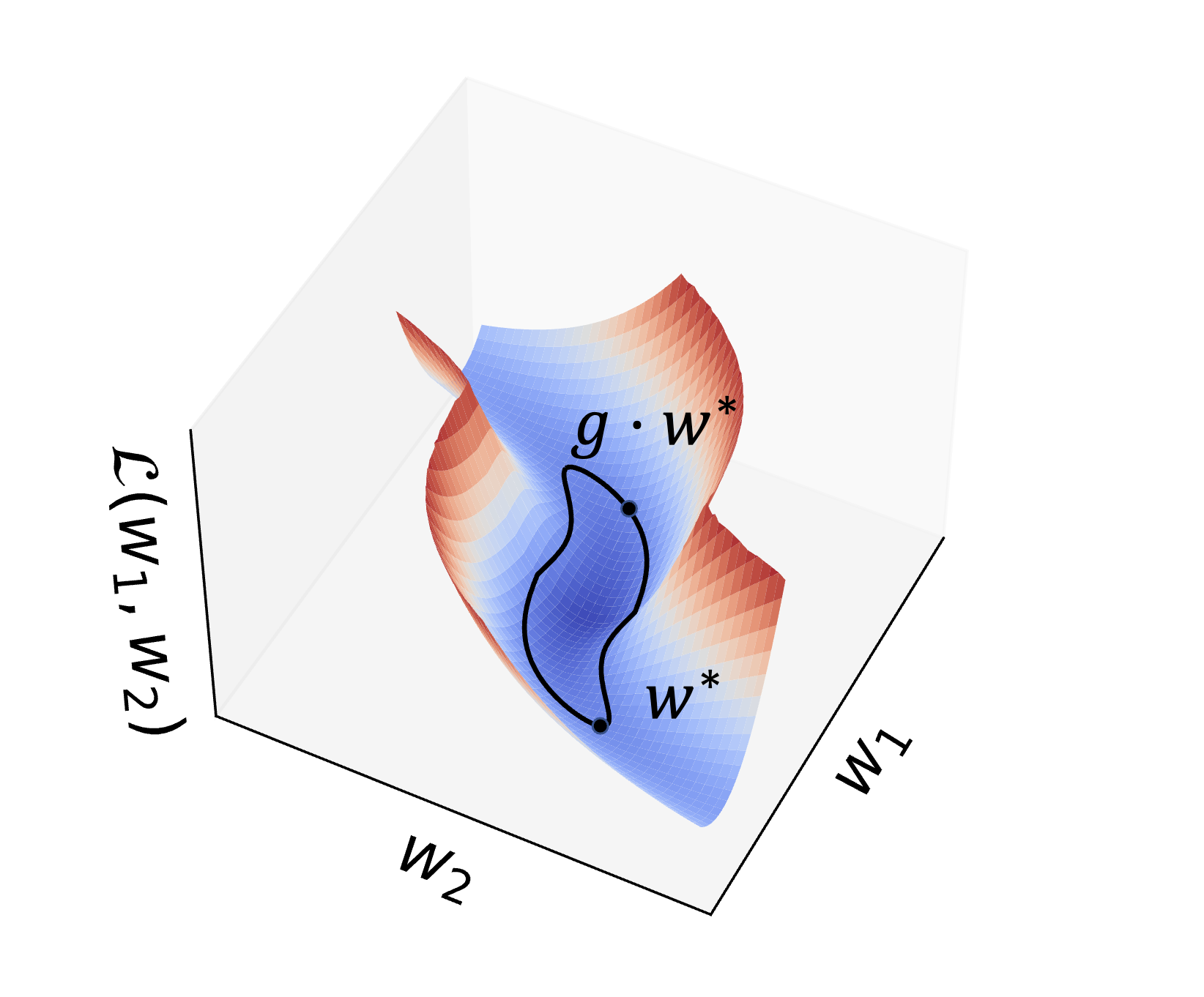
This is interesting because it means for a given set of parameter values at a time step $W^t$ , then we can manipulate them without it changing the output and loss value. That means searching over $g$ would be searching over a level set almost, and we want to find the point that largest gradient norm which is the steepest value. This is Figure 1 from Bo’s paper.

Now it can turn out that certain groups like the permutation group will have no effect on the gradient norm. In addition, the set of permutation matrixes isn’t smooth / continuous so we can’t use gradient based optimization to find the right permutation matrix easily. What is done in practice is use just group defined by $\exp(A)$ , the group of exponentiated matrices. If you don’t recall, the matrix exponentiation operation is:

\exp(A) = I + A + \frac{A^2}{2!} + \frac{A^3}{3!} + \frac{A^4}{4!} + ...

The cool property is $\exp(A)$ is the inverse to $\exp(-A)$ . So we can make $g$ be pre/post multiplying $W_1,W_2$ by $\exp(A), \exp(-A)$ respectively. This allows us to do gradient optimization on $A$ while ensuring that we are within the group. In practice we take the first order Talor approximation and obtain $(I + A), (I - A)$ respectively. This in general won’t guarantee the function value will be the same but the authors observe that the actual change is minimal, and they perform gradient descent to find $A$ that maximizes the gradient norm of $L$ w.r.t $W$ .

In general I find it interesting how we can find different parameterizations of the weights because we can really consider $g,W$ to be the new set of weights, and its interesting to think about how different parameterizations will affect the training trajectory.

Acknowledgments

I got in touch with Bo, and she gave useful feedback on this post!