Exponential Distribution

Formally, the exponential distribution is “the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate.” (Wikipedia).

Motivation

If you believe a Possion Distribution models your data well, then you can use the Exponential distribution to model the time between each “success” of the Poision point process. Since each success is independent of previous successes, the same distribution that models the time between successes can be used to model the time until the first success.

Deriving it

This derivation will rest upon the Binomial distribution. I will list the steps below and then explain the key points.

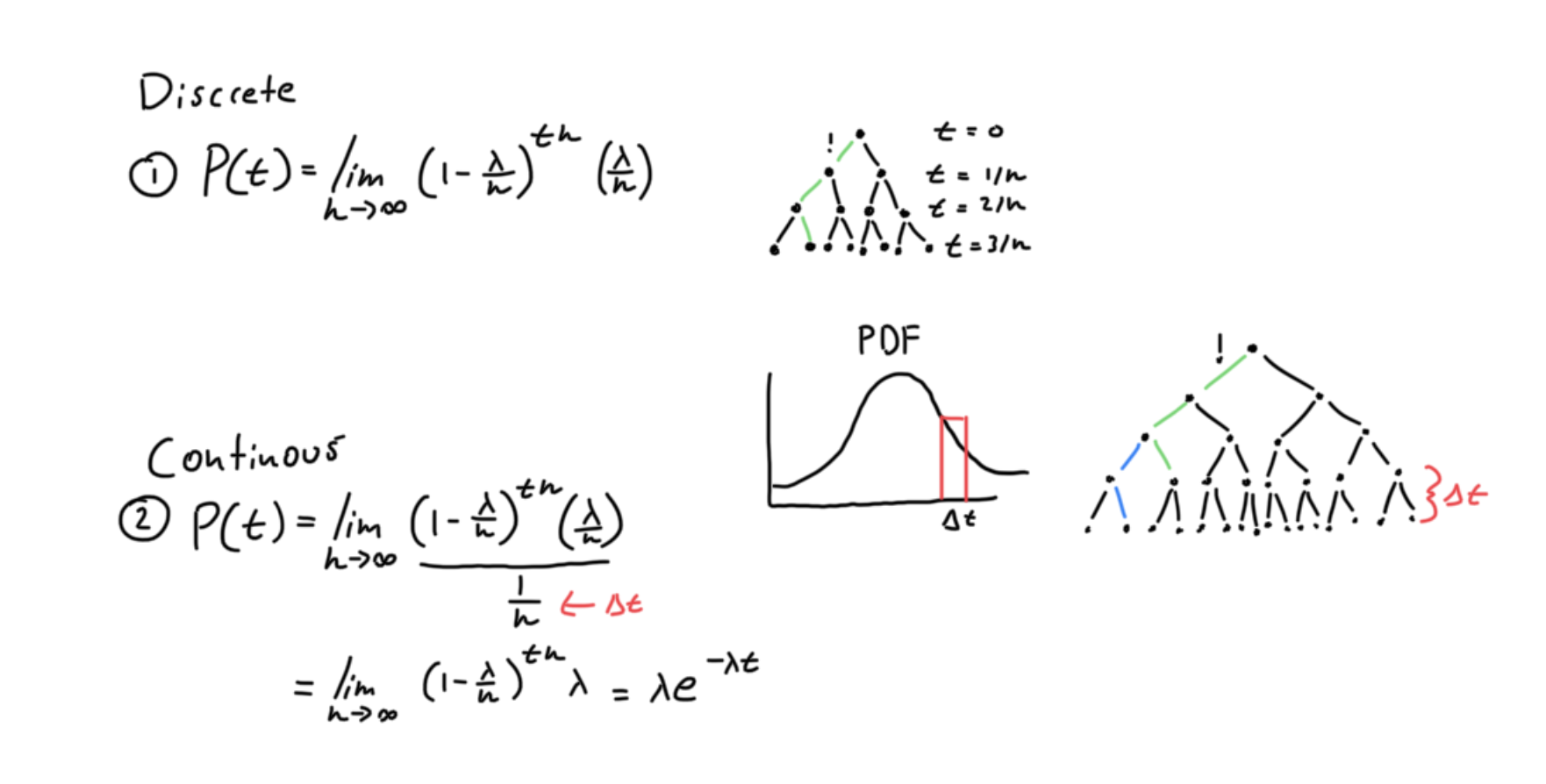
First, we start with equation 1 which is the Binomial distribution with only 1 success. We chop up 1 unit of time into n pieces. As n increases, we obtain a more accurate model since we are increasing the resolution. However, what we have is not a PDF. To transition to the continuous case we need some manipulation. A PDF function can be integrated over an interval to get the probability of that interval. In our discrete case, we can treat the step from t and t+1/n as an interval, where 1/n is the size of each chopped up piece of time. So dividing by the value of that interval will give me the PDF. The value of the interval is the difference in time between two consecutive layers of my tree. This leads us to the continuous equation 2, and with some algebra, you can arrive at the exponential distribution.