Gumbel Softmax

Intro

I have seen Gumbel Softmax (Jang et al) pop up multiple times, and most recently I saw it in the original DALLE paper. Its a neat idea that solves what seems to be a trivial problem. However, this approach is not trivial and its another example of cool math being cleverly applied.

Problem Description

Lets look at where in DALLE Gumbel is used to motivate this problem. They want to maximize $\ln{p_{\theta, \psi}(x,y)}$ and by the ELBO, they derive the lower bound to be:

$\ln{p_{\theta, \psi}(x,y)} \geq \mathbb{E}_{z\sim q_\phi(z|x)}[(\ln{p_\theta(x|y,z)}-\beta D_{KL}(q_\phi(y,z|x),p_\psi(y,z))]$

Here $z$ is a sample from the categorical distribution defined by $q_\phi(z|x)$. This is analogous to a VAE, where $z$ is a latent, but in a VAE the latent space is continuous and in DALLE’s case its discrete (the codebook). Therefore, we can’t slap the same reparametrization trick used in VAEs here. This defines our problem: we want to sample from a $k$ dimensional categorical distribution with unnormalized probabilities $[\pi_1,...,\pi_2]$ and allow gradients to flow through.

Gumbel Softmax

The Gumbel Softmax heavily utilizes the results from (Maddison et al), where the authors present the Concrete distribution: $X \in \triangle^{k-1}$, where $\triangle^{k-1}$ is a $k-1$ dimensional simplex. Intuitively, we want to sample from the vertices of this simplex based on our categorical distribution. The authors define the Concrete distribution as $X_i= \frac{\exp(\log(\pi_i)+g_i)/\tau}{\sum_{j=1}^{k}\exp(\log(\pi_j)+g_j)/\tau}$ where $g_i \sim Gumbel(0,1)$. We will discuss more about what the temperature $\tau$ controls later. Based on this, the joint distribution over the simplex is:

Lets say we have a simple 3 dimensional categorical distribution,

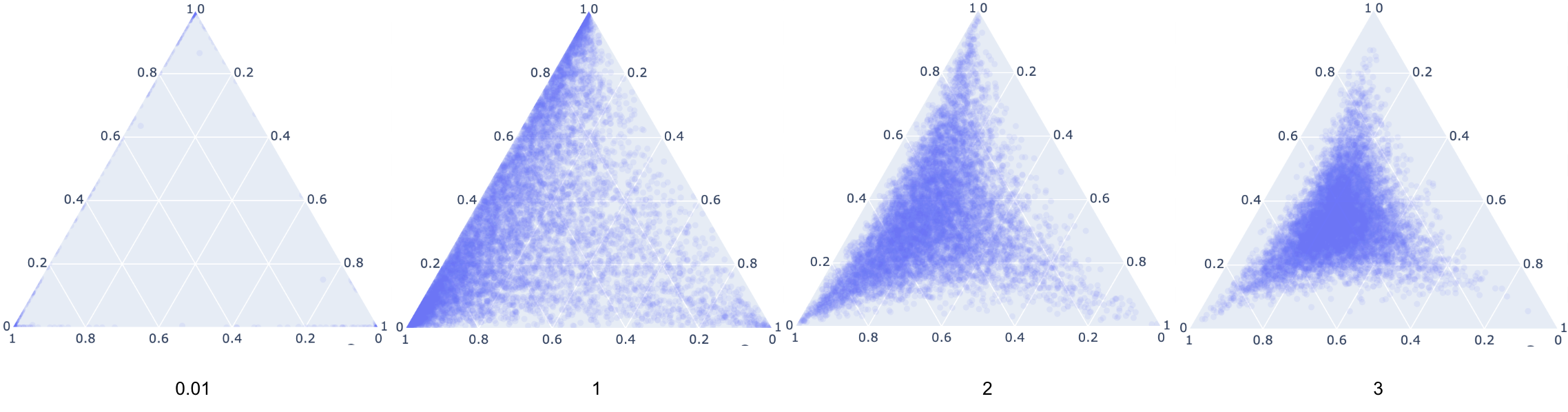
Here are samples for various values of $\tau$ for the unnormalized probabilities,$[1,3,6]$, we can see from the equations and this diagram that $\tau$ controls whether the distribution is sparse or uniform. As $\tau \rightarrow 0$ the distribution will approach sampling from the categorical with probabilities proportional to $\exp(\pi)$. Therefore, if we want to sample from a categorical all we need to do is sample from $k$ Gumbel random variables $g_i$, and then using the above equation for $X_i$ we can construct a sample $X$, and the gradients will not flow through $g_i$ and instead only through $\pi_i$ which is a the output of a previous function. Thus we are all good to differentiate!

Code

import numpy as np
import plotly.express as px

# Gumbel-Softmax Sampler
def sample(pi, t):
    """
    pi: probability vector
    t: temperature
    """
    u = np.random.uniform(0, 1, len(pi))
    g = -np.log(-np.log(u))
    return np.exp((np.log(pi) + g) / t) / np.sum(np.exp((np.log(pi) + g) / t))

t = 3
n = 9999
pi = [1, 3, 6]

samples = sample(np.array(pi), t)
for i in range(n):
    samples = np.vstack((samples, sample(np.array(pi), t)))
# Plot and split samples by columns
fig = px.scatter_ternary(samples[:, 0], samples[:, 1], samples[:, 2], opacity=0.1)
fig.show()