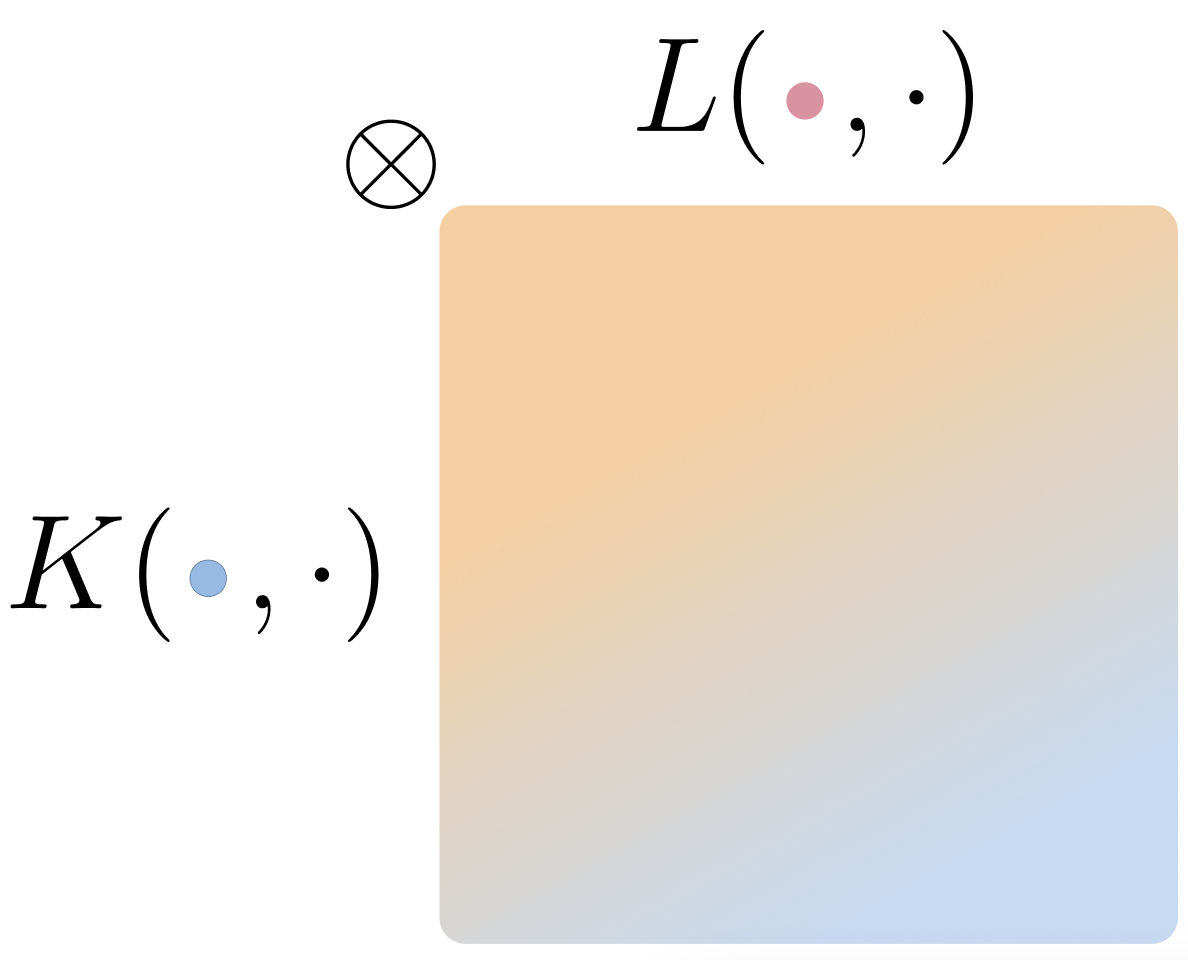Centered Kernel Alignment

After reading the enlightening paper The Platonic Representation Hypothesis and talking to my mentor Jacob Huh, I found the tool of comparing kernels very interesting. Although neural networks are a black box that is hard to interpret, there are ways in which we can compare representational similarity. While this does not provide a complete picture by any means of how representations and networks differ from each other, it does provide a good starting point. The particular method I will be diving into for this post is called the Centered Kernel Alignment.

Problem Setup

If we have a neural network like the one illustrated on the right, then we can tap in to the internal representations in various ways, like average token embeddings at a specific layer, etc. Now the question is given two distributions of representations: $\mathcal{X}, \mathcal{Y}$, how can we compare them?

The Hilbert-Schmidt Independence Criterion (HSIC)

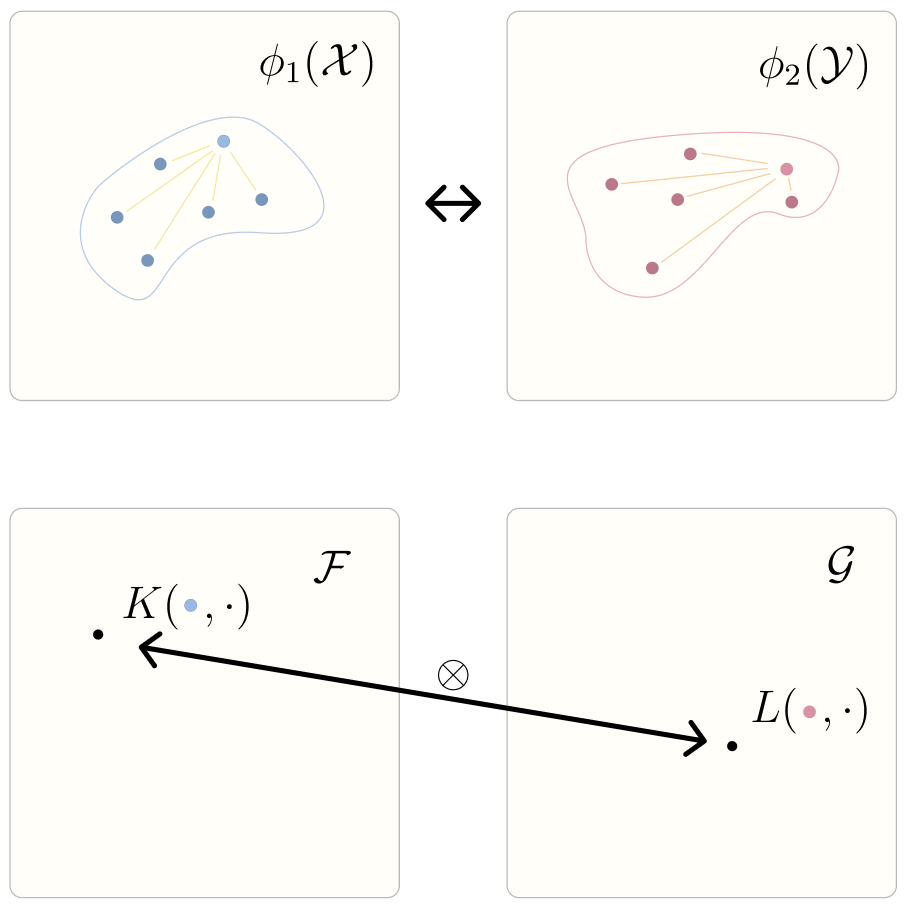
We are going to use some tools, namely, the Reproducing Kernel Hilbert Space (RKHS). By definition, we have a Hilbert Space $\mathcal{H}$, which is a vector space with an defined inner product, and we need a kernel function $K: X \times X \rightarrow \mathbb{R}$ s.t. $\forall f \in \mathcal{H}, f(x) = \langle f, K(x, \cdot) \rangle$. So now for each distribution of representations let's create a different RKHS: $\mathcal{F}, \mathcal{G}$ each equipped with its own kernel $K, L$ respectively, (in practice we use the same kernel function).

This is the Cross Covariance Operator, and it is capturing how “aligned” $\mathcal{F}, \mathcal{G}$ under the distributions $X,Y$ respectively. To add more clarity, by looking at the cross product between the kernels for a sampled pair $x,y$ of inputs, you can tell how “aligned” their kernel distances are the range of $x’s$ and $y’s$ respectively.

To see this the distances between

If we sample some inputs and transform them into their respective representation spaces via $\phi_1, \phi_2$, then associations across their dot product distances is captured by the tensor product in RKHS space. The $i,j$ element in $C_{x,y}$ captures the cross similarity of their associations.

If we have a set of empirical ordered samples $(x_i,y_i)^n_{i=1}$ then we can empirically approximate $C_{x,y}$ via the following equations.

HSIC being equal to $0$ implies that $X,Y$ are independent, and the HSIC is equal to $MMD(P(X,Y) \lVert P(X)P(Y))$, where MMD is the Maximum Mean Discrepancy.

Finally to obtain the CKA, we normalize the HSIC to make it invariant to uniform scaling.

So the important things to note are that if the representations across two networks are the same up to an orthogonal transformation, then the CKA will be invariant to them. It won’t be invariant to any linear transformation. It is also interesting that if $\phi_1, \phi_2$ are identical then:

Here I am abusing notation a bit, and $C_{a,b}$ is an empirical estimation.

References

This blog is great: https://jejjohnson.github.io/research_journal/appendix/similarity/hsic/

https://arxiv.org/pdf/1905.00414

https://www.youtube.com/watch?v=6Xp0i--pg5M

https://www.gatsby.ucl.ac.uk/~gretton/coursefiles/lecture5_covarianceOperator.pdf

ChatGPT