Optimizing the Optimization Trajectory

This is an incomplete blog - and it is an on-going investigation, but there are interesting seeds of thought that is worth sharing. Some of what I will present is from discussions with my mentor Jacob Huh and friend Brian Cheung.

I have been interested in curriculum for a while. In the early days of my PhD I explored how models could potentially benefit from a curriculum - but those explorations did not result in a concrete method. I think my current thought is gradient based optimization does not benefit from the same curriculum human children would benefit from. This raises the question, are there curriculums that would benefit gradient based optimization?

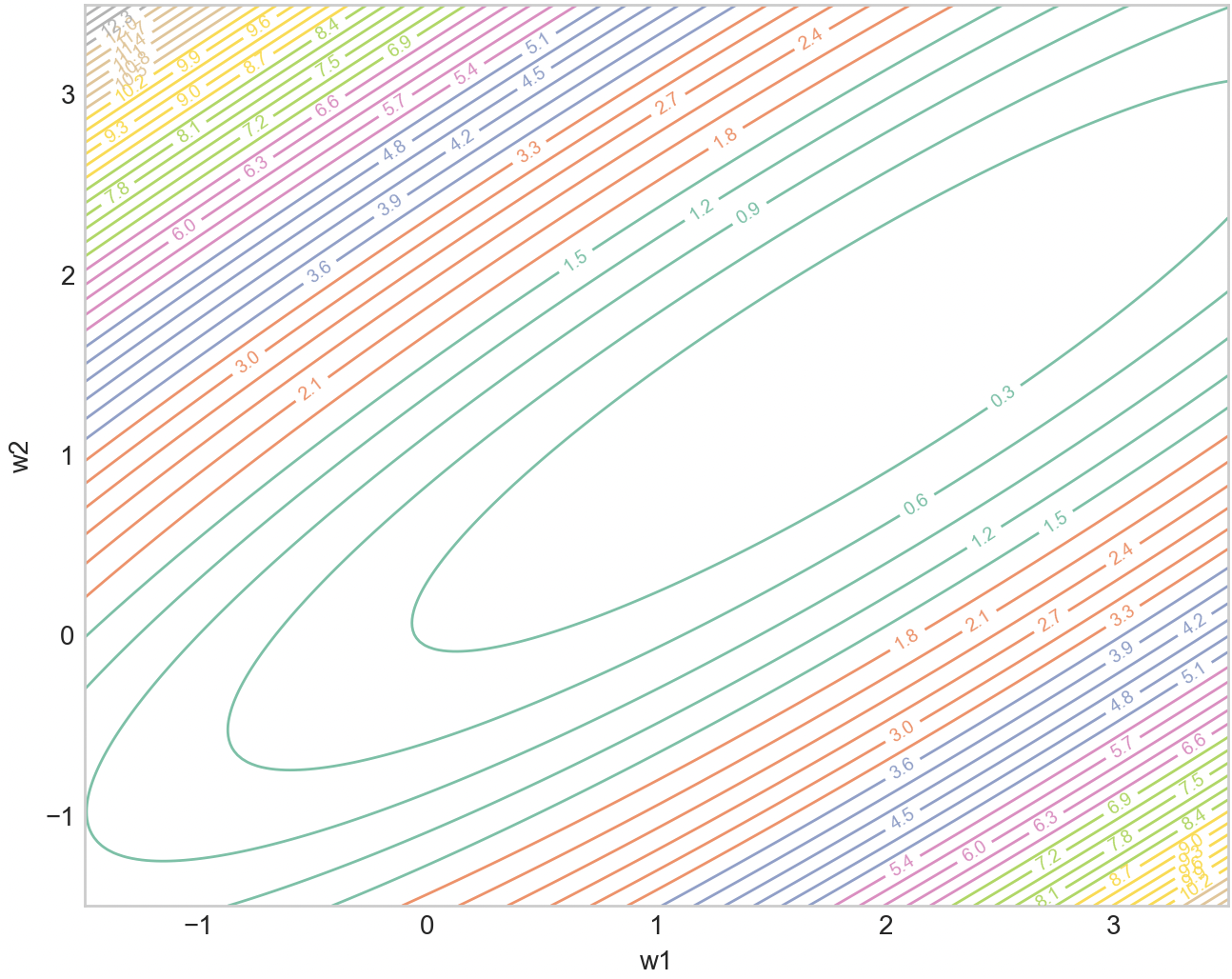
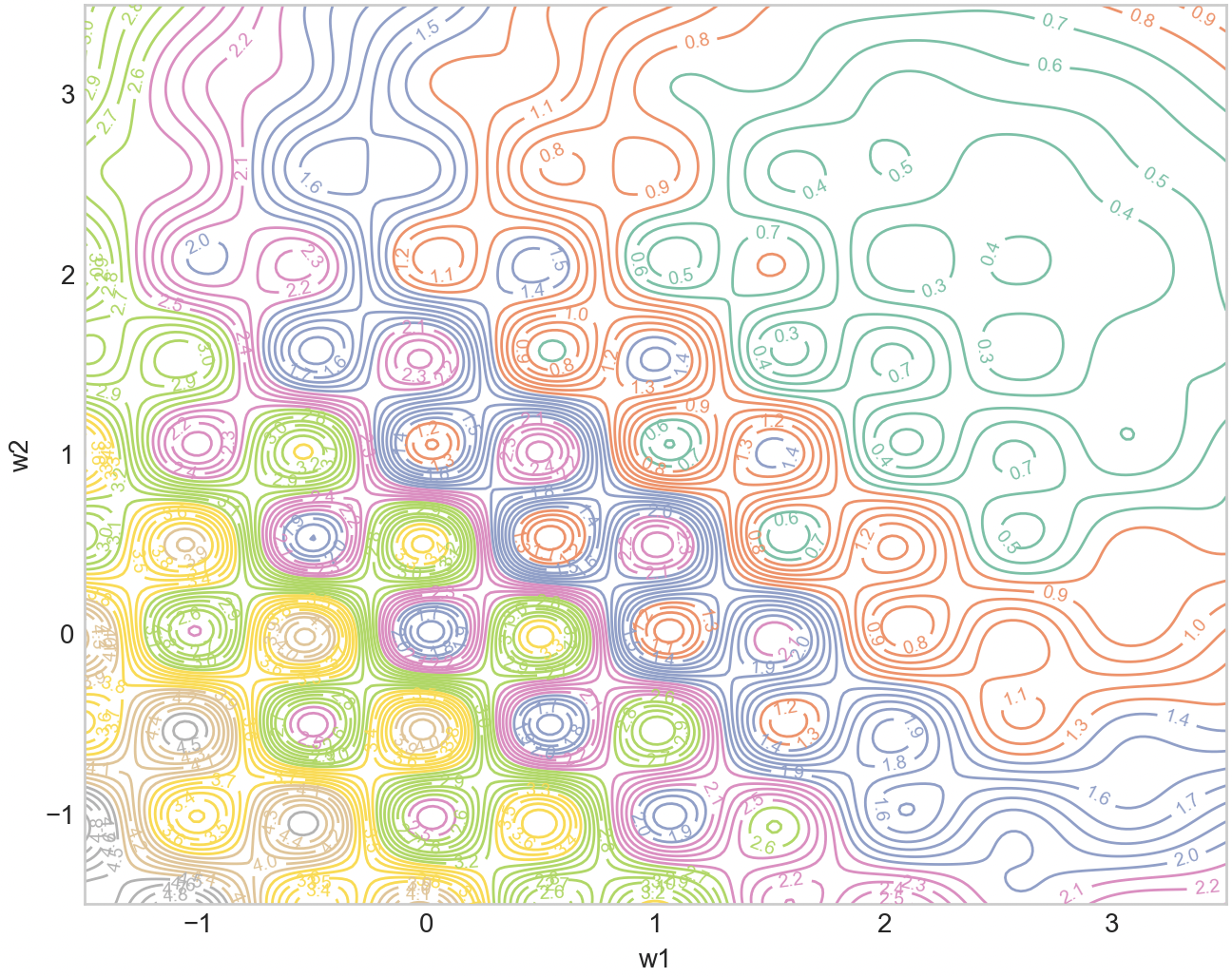
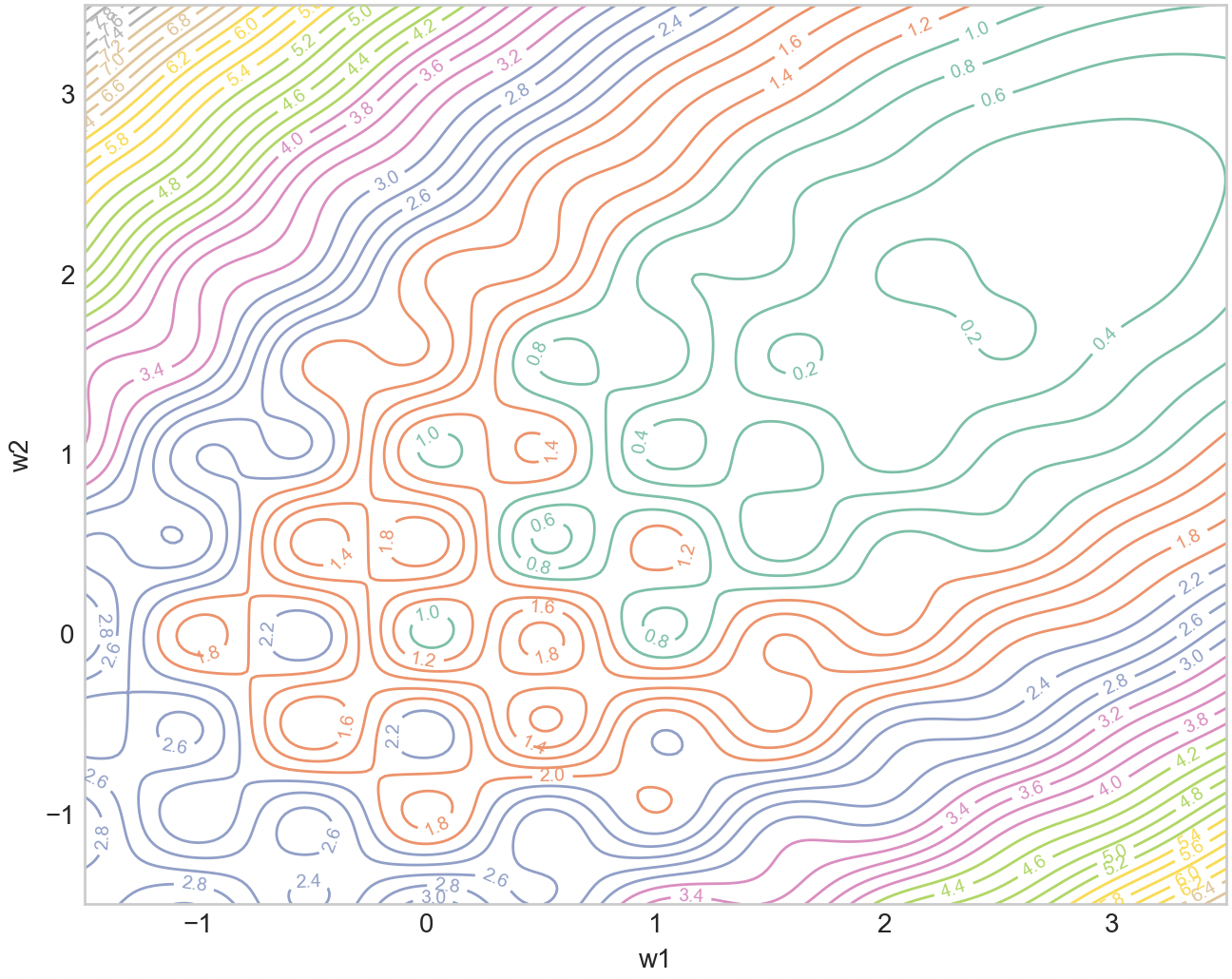
A while ago I had this idea of how we could post-hoc find such curriculums. Let’s say we have a dataset $D$, and model $\pi_{\theta}$. We first train till convergence via the standard stochastic minibatch to obtain $\theta^*$. Then what we can do is look at the linear path: $\theta^* \rightarrow \theta_{\text{init}}$. This straight path has been analyzed in Ian Goodfellow et al’s work: Qualitatively characterizing neural network optimization problems, where the authors find there is a monotonic nature to the loss on that straight path. Moreover, this is the shortest path. This raises the question, how could we have followed this path instead? Well, each datapoint defines its own loss landscape, and we often just average them at random. To simplify things, let’s consider just 2 loss landscapes, the left one being the “easy” one and middle right one is “hard”, and the right one is the averaged (with equal weighting) final landscape.

Revisiting our original question of can we post-hoc find a better ordering using the linear path, let’s now optimize the following objective at each step.

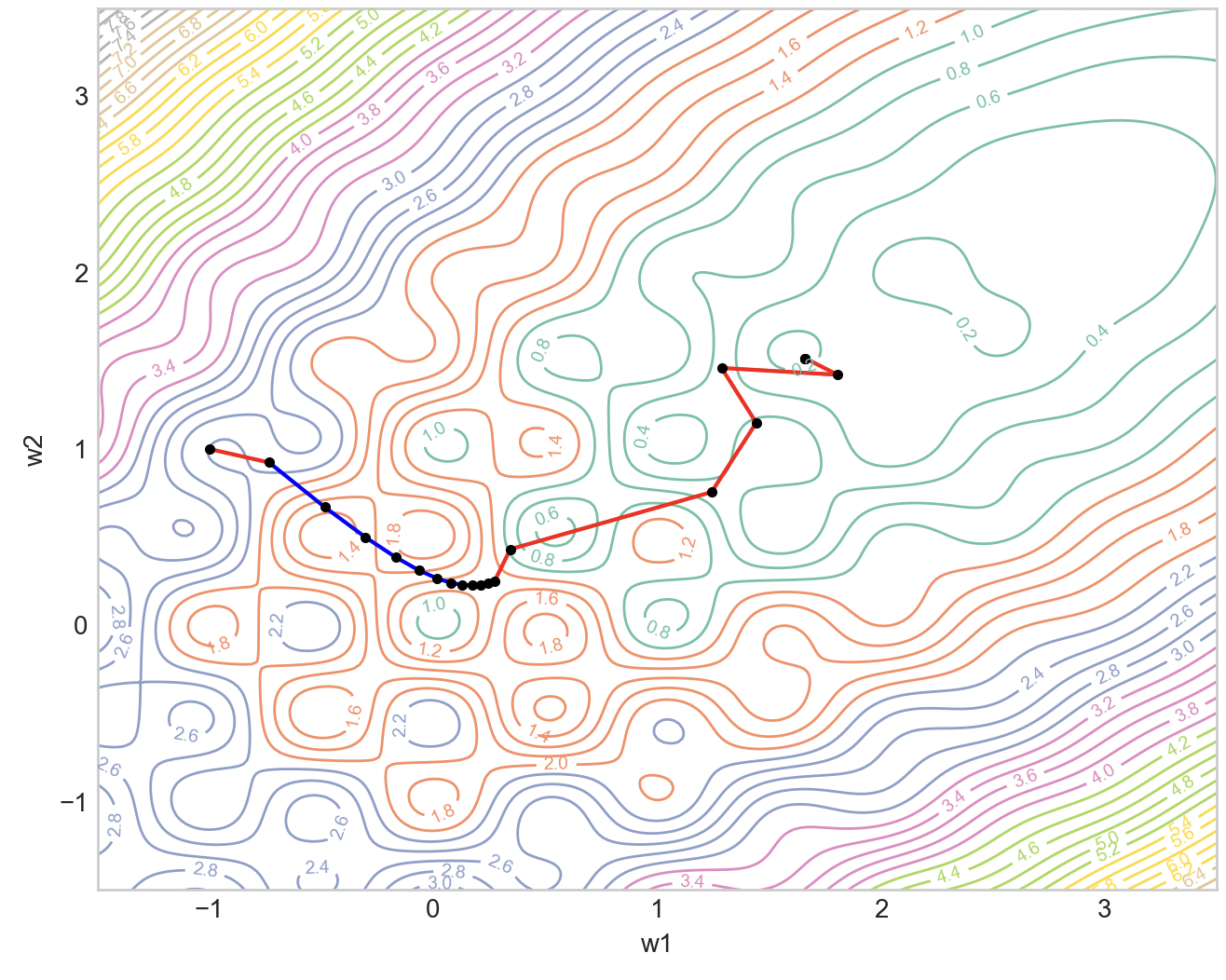
Let $\vec{d} = \theta^* - \theta_{init}$, $\vec{g} = \min\limits_{\alpha > 0, \beta > 0} (\alpha\nabla_{\text{easy}} + \beta \nabla_{\text{hard}})^\top \vec{d}$. Then, we use this as our substitute gradient in our optimization to obtain the left image below, where the blue segments are steps where $\alpha > \beta$ and red when vice versa. The right image is when we randomly weight the gradients from easy and hard to mimic to stochastic minibatch sampling. We can see that the guided optimization does take a more direct path.

Now there are many directions one can further explore the idea. Firstly, I did this in a contrived toy setup where I played with loss landscapes instead of datapoints, so the natural extension is to see how to select minibatches based on gradient alignment to the shortest path. This would be cool if it works because it is using dataset selection to shape the loss landscape. Moreover, if there is a pattern between the types of datapoints, this can be used to train models faster.

Code to reproduce these results: https://github.com/jyopari/dataset_optimization