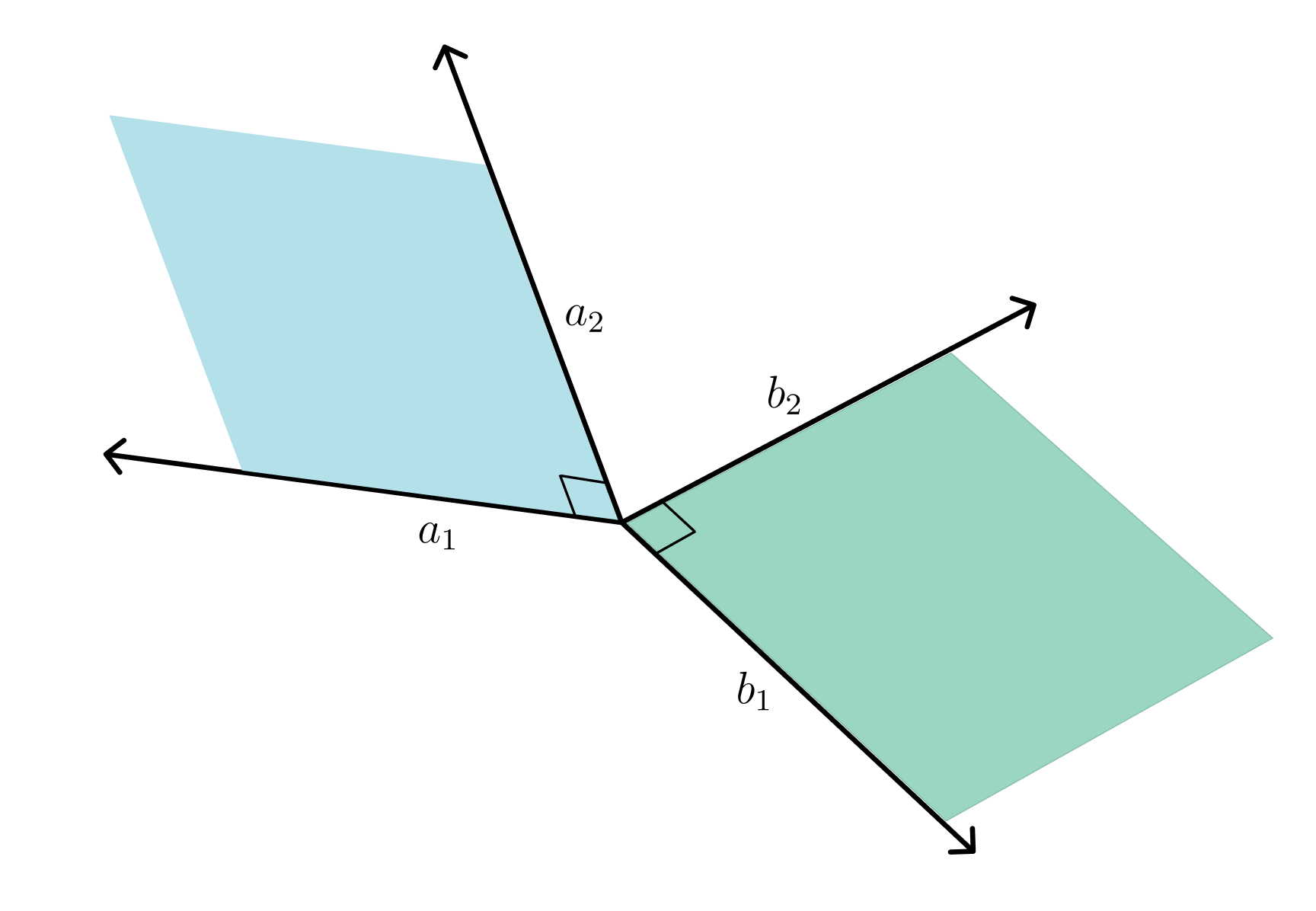
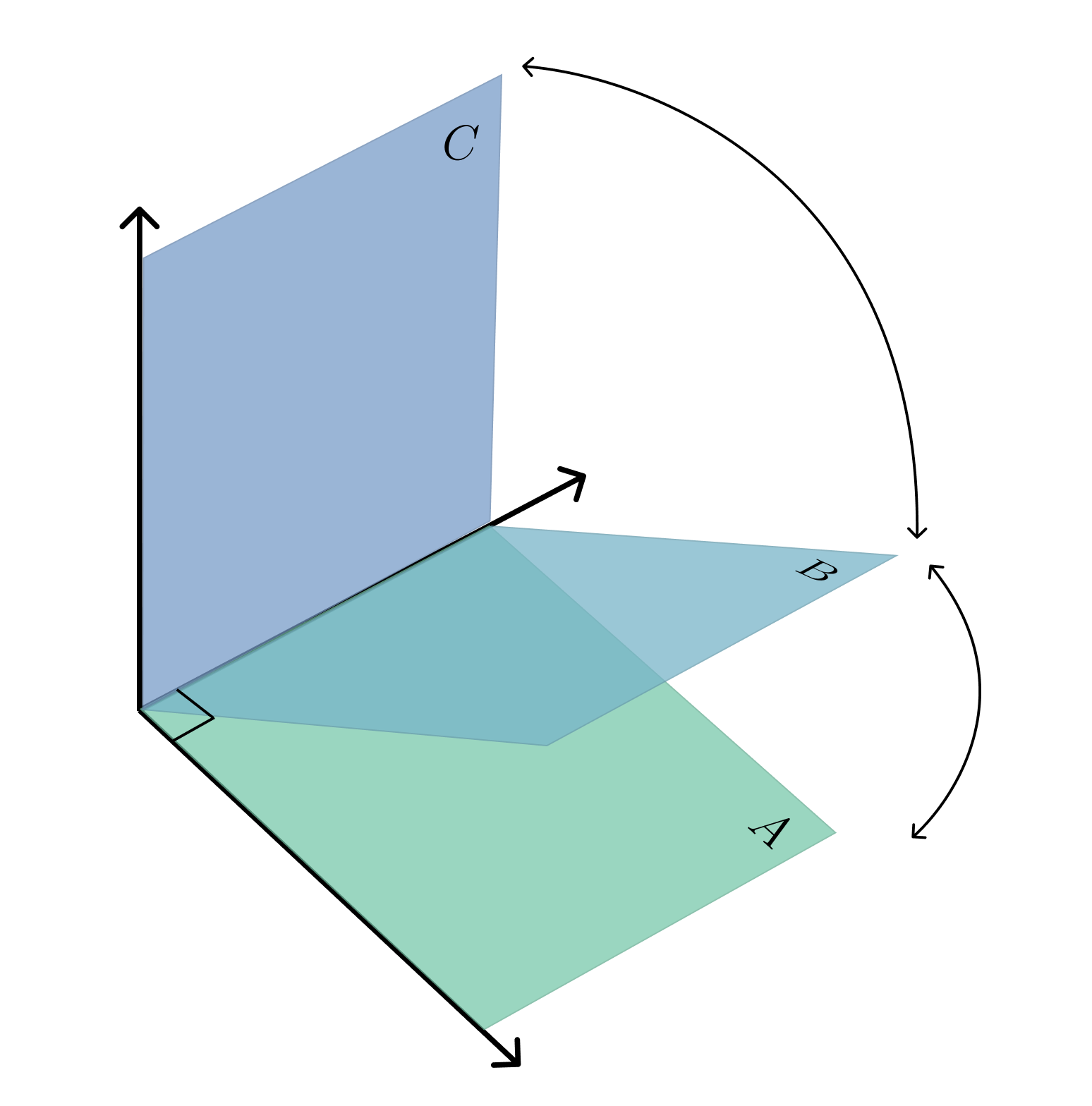
Distances Between Subspaces

This question came up when trying to compare kernels as well as how low dimensional projections change over time. Intuitively it isn’t clear how to create a distance metric between subspaces. For example, lets say we are in $\mathbb{R}^3$, and we have to subspaces $A,B \in \mathbb{R}^2$. To this end, I will try to explain the Grassman distance.

Principle Angles

Then the idea of principle angles is to iteratively find vectors in $A, B$ that have the closest angle. More formally, at iteration $0$, we have the following optimization problem:

We keep repeating this procedure for following iterations with the additional constraint that if we are iteration $i$, then $a_i^Ta_j = 0$ and $b_i^Tb_j = 0, \forall j<i$. Therefore, we are trying to progressively find the most similar orthonormal vectors in $A$ and $B$.

Let $Q_A, Q_B$ be orthonormal basis for $A,B$ respectively. Then from our previous iterative algorithm, let $a_0 = Q_Ax_0, b_0 = Q_By_0$, so we want to maximize $(Q_Ax_0)^T(Q_By_0) = x_0^TQ_A^TQ_By_0$. Let’s compute the SVD of $Q_A^TQ_B = U\Sigma V^T$. Substituting yields, $x_0^TU\Sigma V^Ty_0$. Therefore, if we align $x_0$ with the top singular vector in $U$ and $y_0$ with the top singular vector in $V$, then the resulting value will be the largest singular value $\sigma$. In fact the singular values are the ordered solutions to the aforementioned iterative optimization procedure (think about why that is the case). The Grassman metric is now defined as:

I am not going to prove why the triangle inequality holds for this to be a metric, but you can look at some of the resources I linked below. I might revisit it and add it to the blog later.

Code

import torch
import math

def grassman(A, B):
		# get orthogonal basis
    Q_A, R = torch.linalg.qr(A)
    Q_B, R = torch.linalg.qr(B)

		# get singular values
    _, S, _  = torch.svd(Q_A.T @ Q_B)
    # cosine inverse
    thetas = torch.arccos(S)
    # return norm
    return torch.norm(thetas, p=2)

A = torch.tensor([
    [1, 0],
    [0, 1],
    [0, 0]
]).float()
B = torch.tensor([
    [math.sqrt(0.5), 0],
    [0, 1],
    [math.sqrt(0.5), 0]
]).float()
C = torch.tensor([
    [0, 0],
    [1, 0],
    [0, 1]
]).float()
>>> grassman(A,B)
tensor(0.7854)
>>> grassman(A,C)
tensor(1.5708)
>>> grassman(C,B)
tensor(0.7854)

References

https://en.wikipedia.org/wiki/Grassmannian

https://kristianeschenburg.netlify.app/post/comparing-subspaces/

https://web.ma.utexas.edu/users/vandyke/notes/deep_learning_presentation/presentation.pdf

https://galton.uchicago.edu/~lekheng/work/schubert.pdf