Towards Self-Editing Models : Part 1

Motivation

A recent trend in machine learning research has focused on test-time training and, more broadly, on methods that allow models to adapt to new examples. One particularly intriguing direction in this area is enabling models to self-update, removing the need for external optimization processes. Although appealing in theory, accomplishing this is non-trivial, and in this article I propose thinking of more expressive self-updating mechanisms.

Related Work on Self-Updating Mechanisms

Several lines of work provide insights into how models might update themselves. For instance, my colleague Ekin has a very interesting paper, "What Learning Algorithm Is In-Context Learning? Investigations with Linear Models". The authors demonstrate that:

"Transformers can implement learning algorithms for linear models based on gradient descent and closed-form ridge regression."

Another paper I like is "Trainable Transformer in Transformer" by Sanjeev Arora’s group, which shows how the forward, backward, and update steps of a smaller transformer can be simulated within a single forward pass of a larger transformer.

These approaches, while highly creative, prompt an important question: What if we want the inner model to grow—i.e., to capture an increasingly complex function class over time?

Conceptual Framework: Growing Models

Consider the diagram below:

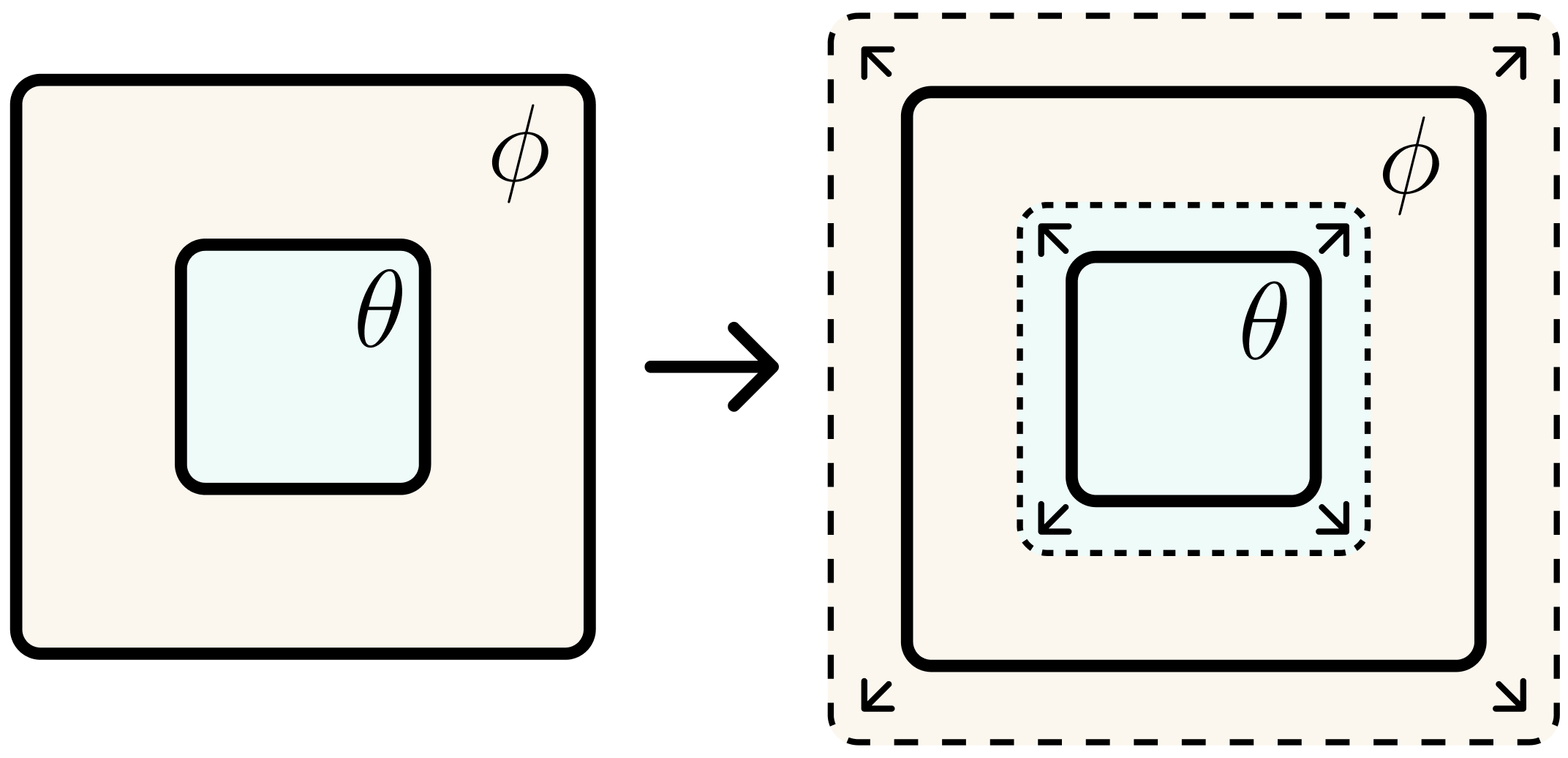
On the **left**, the larger model, denoted by φ, is responsible for optimizing the parameters of the inner model, θ. If we want θ to become more complex over time, φ must also grow to support and guide that increased complexity. This nesting of inner and outer models introduces significant challenges: the update mechanism for θ is bound to φ’s capacity to represent and manipulate growing parameter sets.

Towards a Single Self-Updating Model

Rather than maintaining a nested structure ( $\phi$ updating $\theta$ ), we can envision a single model that self-updates—and even grows—entirely on its own. If we rely solely on gradient descent as the desired update, the model can only update a small sub-component of itself at each step as shown by the aforementioned papers. Yet gradient descent is not our only option. In principle, a model could learn other and efficient mechanism for self-updating, potentially bypassing the limitations of an external optimizer.

With that in mind, the following sections explore how transformers, chain-of-thought (CoT) reasoning, and related paradigms might inspire the design of architectures that adapt and expand.

The Case with Transformers and Chain-of-Thought (CoT)

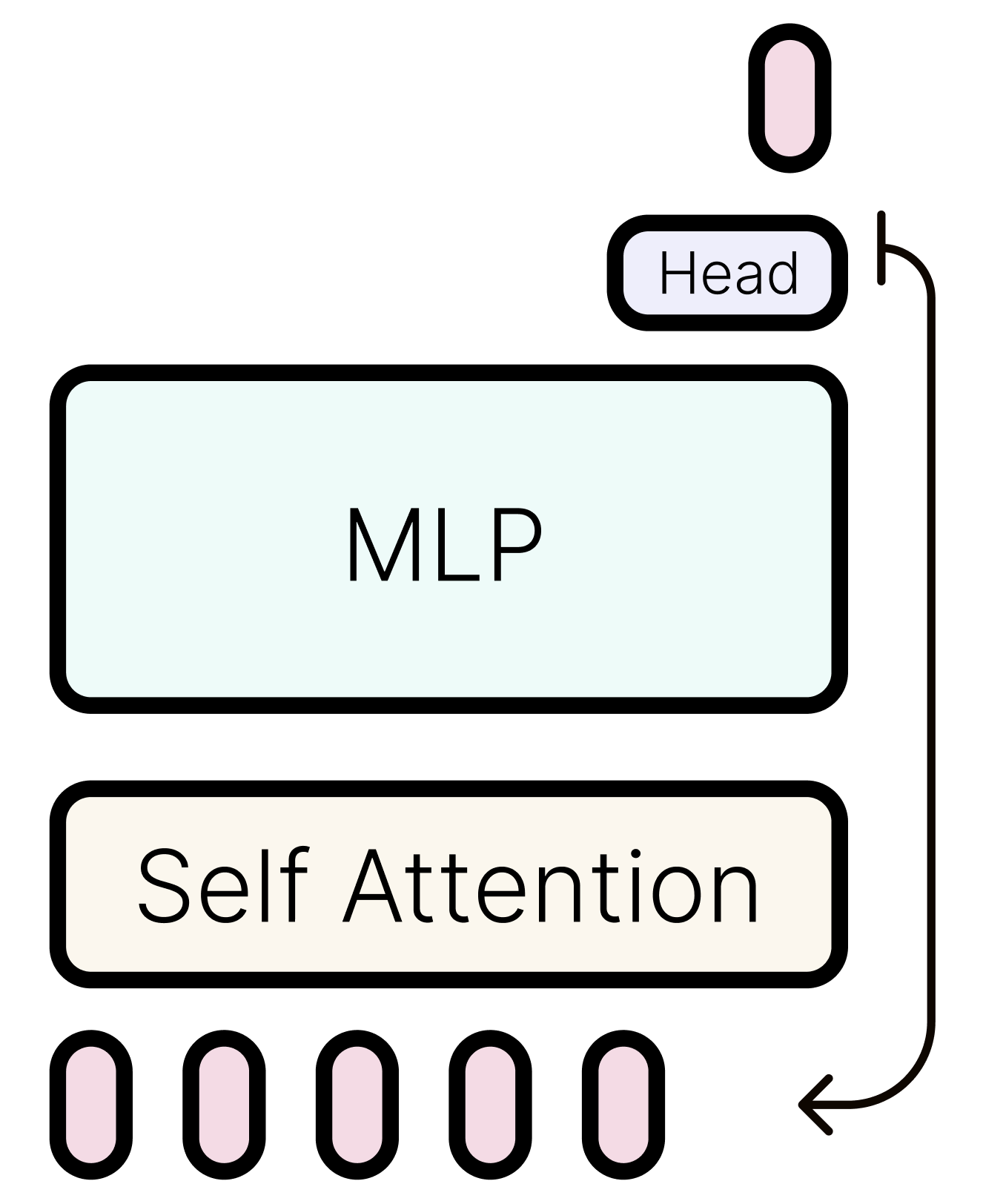
If we think about modeling any function with a Transformer, one line of thought is can they behave like interpreter and compute any inputted program? To this end, a thought-provoking paper, “The Expressive Power of Transformers with Chain of Thought” by Will Merrill, demonstrates that with slight modifications to the standard transformer decoder, one can simulate both finite automata and Turing machines. In this analogy, the CoT reasoning serves as the Turing machine’s tape, while the MLP block encodes the transition function—the “program” being executed.

However, a critical limitation arises from the static nature of the MLP block. Because its parameters remain fixed during inference, the program encoded by the transformer cannot modify itself dynamically. The model can simulate pre-defined computations but cannot self-edit its own transitions or logic. This leads us to the question:

What can transformers model over time if they cannot change their own weights - but only the context.

Transformer Dynamics and Computational Scaling

In a standard transformer decoder generating text auto-regressively, each predicted token must attend to all previous tokens. This implies that the amount of computation grows with the sequence length. Specifically, the self-attention mechanism $\sigma(qK^\top)V$ includes an increasingly large context as the sequence unfolds. Consequently, the model can represent increasingly complex functions simply by attending to more tokens - hence the higher FLOPs that are paid.

Even in simplified cases—such as “hard” attention where $k=1$ self-attention can theoretically model arbitrary mappings by acting like a hash table. With the addition of the MLP block, the model can transform these mappings into richer representations. Stacking multiple layers adds further expressive power. Below is an illustrative example showing how linear attention can be formulated in a recurrent manner, to provide perspective on how the function changes.

\begin{aligned} &\textbf{Linear (no-softmax) attention recurrence:}\\[6pt] &U_{t+1} \;=\; U_t \;+\; k_{t+1}\,v_{t+1}^\top, \quad w_{t+1} \;=\; w_t \;+\; k_{t+1},\\[4pt] &O_{t+1} \;=\; \frac{\,q_{t+1}^\top\,U_{t+1}\,}{\,q_{t+1}^\top\,w_{t+1}\,}. \end{aligned}

Although it differs from standard softmax-based self-attention, it highlights how the function changes when a new token is added. And the direction I want to think about is how can we make more expressive function updates.

A notable constraint of standard transformers lies in their inability to revise their context history. This is analogous to writing code sequentially without ever returning to edit earlier lines. In contrast, a human programmer routinely refines and updates previous code to correct errors or optimize performance. Transformers, however, process the context in a strictly forward manner, potentially limiting their capacity.

The End Goal

Ultimately, we want a model that runs and continually edits itself—much like a Python script that automatically modifies its own source file at the end of each execution. In deep learning terms, the challenge is to design and train models that can modify both their parameters and their computational structure over time, without relying solely on an external optimizer.

The key question thus becomes:

How do we equip transformers—or any deep learning architecture—with the capacity to function like a self-editing program?

Addressing this question requires breaking away from purely static architectures and exploring mechanisms that allow models to rewrite both their intermediate states and the “program” they encode. Below I listed some directions I think are worth considering.

Directions Forward

Modular Networks for Self-Editing: Modular networks decompose a model into subroutines—akin to functions in a programming language—each with a stable, well-defined interface. A controller oversees how these modules are created, combined, or replaced, enabling the system to incrementally build more complex functions. The “edit” parameterization becomes a blueprint for constructing new modules or inserting function calls, allowing the model to expand its functionality over time while preserving robustness and clarity at the interfaces.

Token-Driven Updates

A powerful approach is to treat tokens themselves as executable instructions that directly modify the model’s function. Rather than mere following the fixed computation of self attention, these “edit tokens” are interpreted by a specialized mechanism or “interpreter,” which translates them into structural or parameter updates. By embedding edits into the model’s own generation process, the system gains in-context self-modification capabilities: it can create new functions, alter module connections, or adjust parameters on the fly. This mechanism mirrors how a programmer edits code—except that the instructions here are produced and consumed within the same architecture. Key challenges include ensuring valid updates, preventing runaway changes, and balancing the expressive power of edit tokens with the stability needed for reliable execution.

Differentiable Parameterized Edits

Up to now, we’ve mainly considered discrete structural edits—like adding or removing layers. But could we instead continuously modify a network’s architecture, beyond just adjusting parameters? For instance, can we devise a gradient-based process that gradually morphs a model’s structure—expanding or contracting its capacity in a smooth, differentiable manner? This might merge the interpretability of explicit structural changes with the finer control of continuous optimization, opening new pathways for self-editing architectures.

Summary

Parameterizing a self-editable model opens new frontiers in machine learning. Meta-learning training frameworks can equip these models to adapt their own update rules, but achieving scalability and reliability demands efficient approaches to meta-optimization and thinking of alternatives. Striking the right balance between complexity, interpretability, and stability remains an open challenge.

Key Takeaway: I think the key punch lines I am thinking about is:

A mechanism / parameterization for specifying edits (the “language” of self-modification).
- Mathematically, how can we understand the class of functions that can grow over time from a seed function

References:

Ekin Akyürek et al., "What Learning Algorithm Is In-Context Learning? Investigations with Linear Models", 2022.

Sanjeev Arora et al., "Trainable Transformer in Transformer", 2023.

Will Merrill, "The Expressive Power of Transformers with Chain of Thought", 2023.

Katharopoulos et al., "Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention", 2020.