Sequence Modeling / Memory

Introduction

I have been fascinated about memory for a long time. I think its irrefutable that it is a core component of human intelligence, and consequently how can we develop architectures that also have long term / life long memory? Here I will keep a record of some recent papers on this topic, and they will be roughly in the high level since there are many different broad approaches and I want to capture their essence all in one page.

Sequence Modeling with Multiresolution Convolutional Memory

This is a fascinating paper because it uses the idea of wavelet transform. I won’t go through the details of what the wavelet transform is, but to provide a conceptual illustration: a wavelet is a family of functions derived from a mother wavelet ψ(t)\psi(t), that satisfies certain properties like having an average of 0 and a finite energy.

∫−∞∞ψ(t)dt=0,      ∫−∞∞∣ψ(t)∣2dt<∞\int_{-\infty}^{\infty}\psi(t)dt = 0, \,\,\,\,\,\, \int_{-\infty}^{\infty}|\psi(t)|^2dt < \infty

The cool part about wavelet transform is that it hierarchically decomposes the function down. This is done by creating a family of functions based on the mother wavelet

ψj,k(t)≜2j/2ψ(2jt−k)\psi_{j,k}(t) \triangleq 2^{j/2}\psi(2^jt-k)

From this we can obtain a orthonormal functional basis. For an example, see the Haar Wavelet. In the above definition jj represents which level of the decomposition we are in, and kk  the shift / position within that level. Here is a illustration of the hierarchy

From Wikipedia

The paper goes into detail on how to obtain the coefficients for the basis functions, and a key detail is they don’t use a fixed filter which would correspond to using a specific wavelet. Instead they make them learnable. However, storing the coefficients would scale quadratically with the sequence length. Therefore, they selectively only store a subset of the coefficients.

Figure 2 from the paper

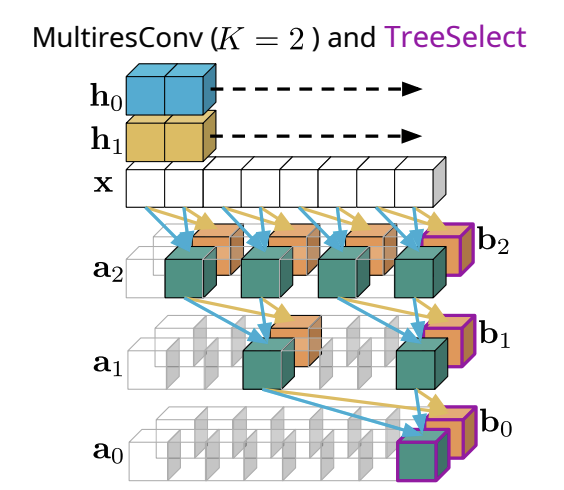
They explore two methods for the coefficient selection and notice comparable results.

My Takeaways

I like this paper because it uses the intuition of how wavelets can hierarchically decompose a signal down at different resolutions in different sections of the signal. Therefore, you can selectively choose what is the pertinent information you want to retain for your task. I think a future direction would be more sophisticated TREESELECT mechanisms that are learnable.