Why Is the Gradient the Direction of Steepest Ascent?

It’s an understatement to say gradient descent is core to machine learning. The phrase “we step down in the steepest direction” is ubiquitous in gradient descent explanations. But why is the gradient the direction of steepest ascent or descent? Note, this explanation is a bit more lengthy than others, such as this fantastic video, because I wanted to use Lagrange Multipliers, and I think it’s important to see the problem from different perspectives.

Explanation

Let’s say we have the following function f. You could think of this as your loss function for your model.

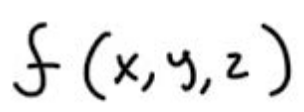
Directional Derivative

Now we are not going to look at it’s gradient per say, but instead f’s directional derivative. This is just measuring the change in f with respect to the change in x,y,z in a certain direction. That direction is going to be vector v.

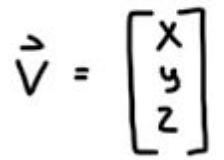
The directional derivative is L

Now since we are just interested in direction, we want to constrain v such that its length is 1. You can think of this as a sphere since we are in 3D. Here is the constraint written down.

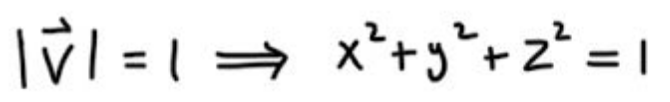
I am going to define the function g as the length of v, and it is equal to 1. Now what we want to maximize is the directional derivative because that would mean we have chosen the right v such that stepping in the direction v will raise us to the greatest elevation.

Lagrange Multiplier

We want to maximize L constrained on g. This is what the Lagrange Multipler was made for. Remember that at critical values, the gradients of L and g will point in the same direction, but with different scales. This can be represented by the following equation.

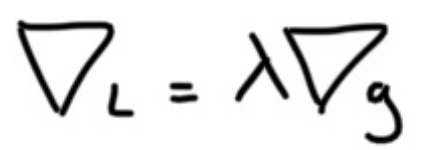
In vector representation,

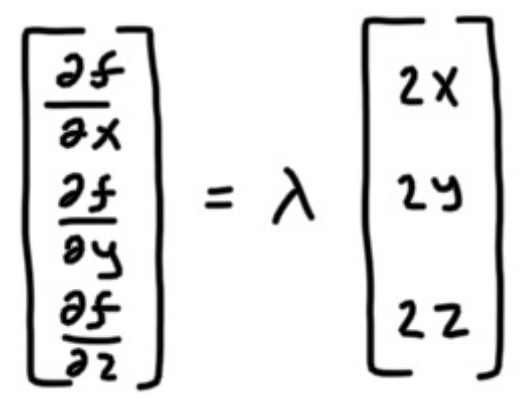
So we have the following set of equations.

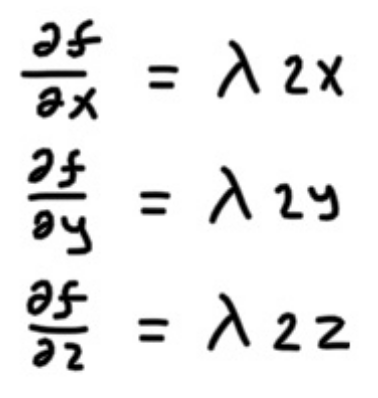
Now remember our original constraint g, let’s write that down again, followed by some substitution.

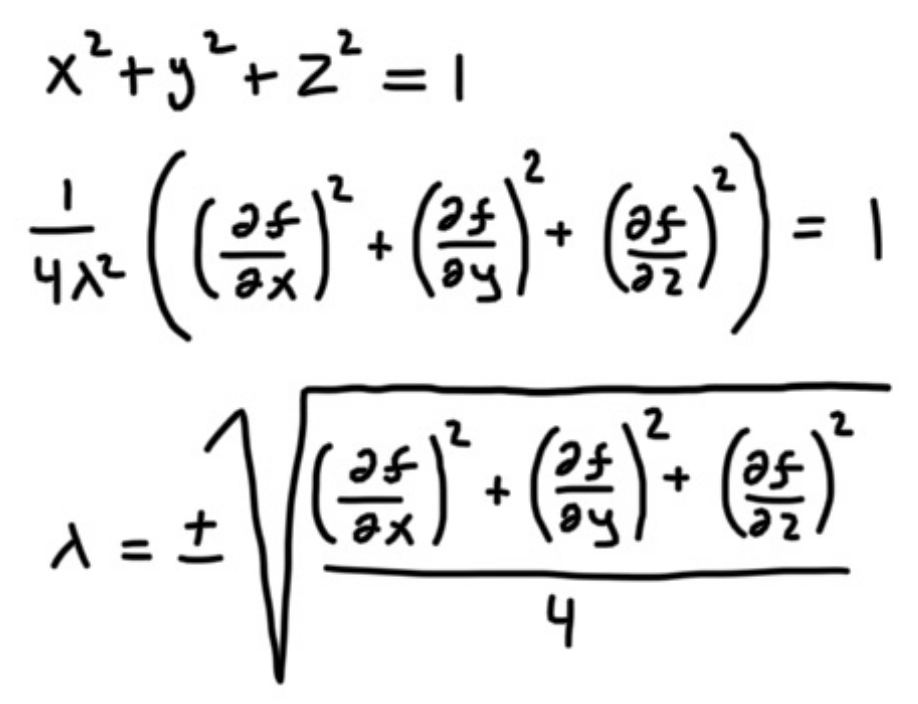
We have now solved for . Notice has a positive and negative value. We can substitute in

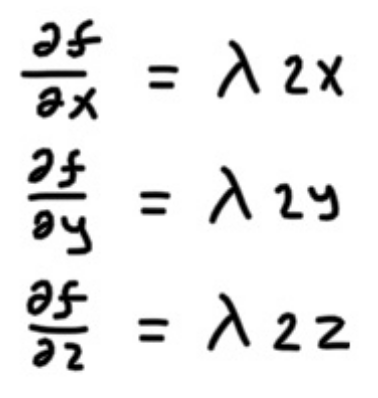
Thus we can solve for x,y,z, and consequently obtain our v. But can be 2 values, which makes sense, since the Lagrange Multiplier finds the critical values, then one will be the steepest assenstion and the other will be the declination. Thus we find v points in the same direction as the gradient of f.