Peculiarities of Mixture-of-Expert Optimization

When I began my PhD, my mentor Jacob Huh , advisor Pulkit Agrawal and I were captivated by the idea of modularity—architectures that could adapt at test time by swapping or recombining components. This curiosity led us to Mixture of Experts (MoE) models: inherently modular structures where a router chooses a subset of experts to process each input. But as we dug deeper, we discovered something odd—router optimization in MoEs is subtly broken.

We asked ourselves: What if the router is optimizing the wrong objective entirely? And why are routers expected to both select experts and weight their outputs?

Our blog explores these peculiarities. While our fixes didn’t improve large-scale MoE pretraining, they revealed lessons that may be useful insights to others working on model stitching or modular architectures.

The Standard MoE Routing Objective Is Mismatched

In a standard MoE layer, we route input tokens to a sparse subset of experts. This can be written as:

$g(X, R) = \sum_{n=1}^{N} R_n \odot E_n(X)$

$X \in \mathbb{R}^{\text{tokens} \times d}$ is the input

$E_n(\cdot)$ is the n’th expert

$R_n \in \mathbb{R}^{\text{tokens} \times 1}$ is the router’s output (probability or score)

$\odot$ denotes element-wise multiplication

Routers are typically parameterized as:

\pi(X) = \text{top-}k(\text{softmax}(X W_R))

where $W_R \in \mathbb{R}^{d \times N}$ .

Now, if we freeze the experts and optimize only the router, the ideal routing objective is:

\min_{\pi} \mathbb{E}_{X, Y, R \sim \pi} \left[ \mathcal{L}(F(X; R), Y) \right]

This is equivalent to a contextual bandit problem, where reward is defined as:

r_t = -\mathcal{L}(F(X; R), Y)

However, standard optimization of MoEs under sampling the router during training does something else. It effectively optimizes:

\min_{\pi} \mathbb{E}_{X, Y} \left[ \mathcal{L}\left(F\left(X; \mathbb{E}_{R \sim \pi}[g(X, R)]\right), Y \right) \right]

This expectation inside the model is problematic because if the downstream model is nonlinear (which it usually is), this approximation is no longer valid. As a result, routers trained this way may not learn the optimal expert selection strategy.

Router Policy Optimization (RPO)

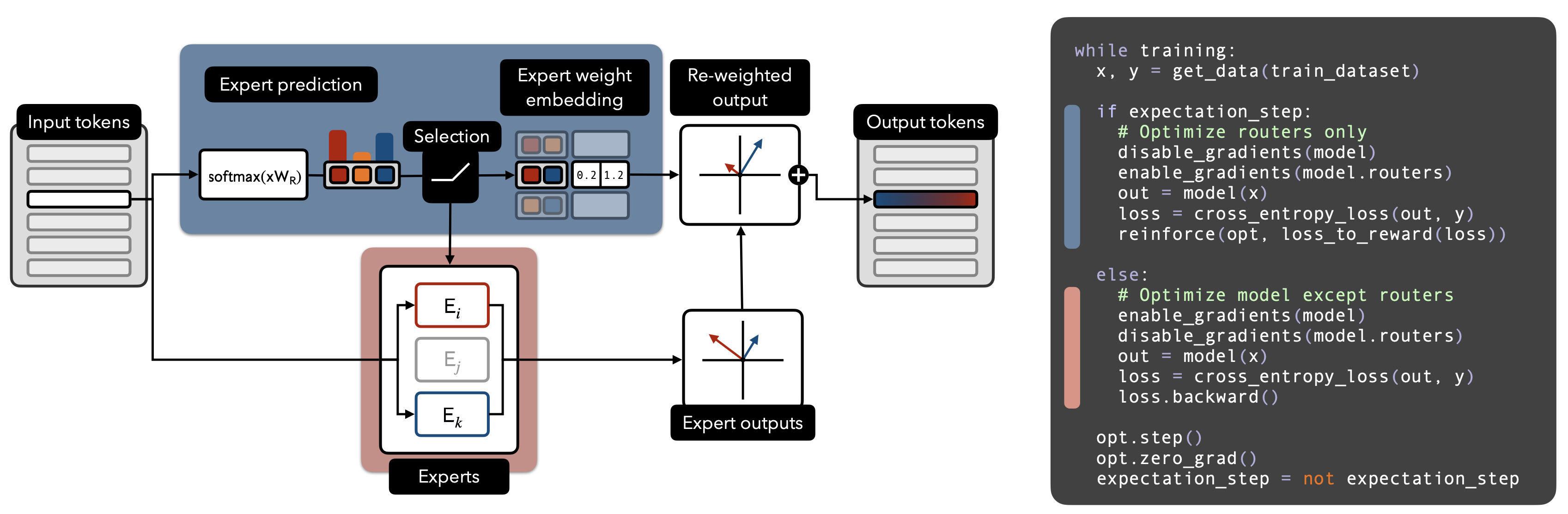
To address this mismatch, we proposed Router Policy Optimization (RPO). RPO reframes routing as a reinforcement learning problem (this isn’t new - but how we parameterize is novel)

First, select a subset of experts using a categorical policy:

\pi_{\text{SELECT}}(s | x)

Then, predict the weights over those experts using a separate Gaussian policy:

\pi_{\text{WEIGHT}}(\alpha | s)

We alternate between:

E-step: Fix the experts, optimize the router via REINFORCE using the loss as the negative reward.

M-step: Fix the router, optimize the rest of the model via empirical risk minimization.

This coordinate descent structure helps isolate the learning of routing from that of expert specialization.

Decoupling Selection from Weighting

Standard practice uses the router probabilities both to select experts and to weight their outputs:

\hat{y} = \sum_{n \in \text{TopK}} p_n \cdot E_n(x)

But this coupling is problematic. If the optimal weighting requires a lot of one expert but a small amount of another then standard optimization won’t choose the small weighted expert. Here is a simple regression task to show there where the red star is the target - the experts are frozen vectors. Then we plot what standard MoE optimization does over time steps (white → blue). As you can see, it is sampling around the experts that are most closest to the target.

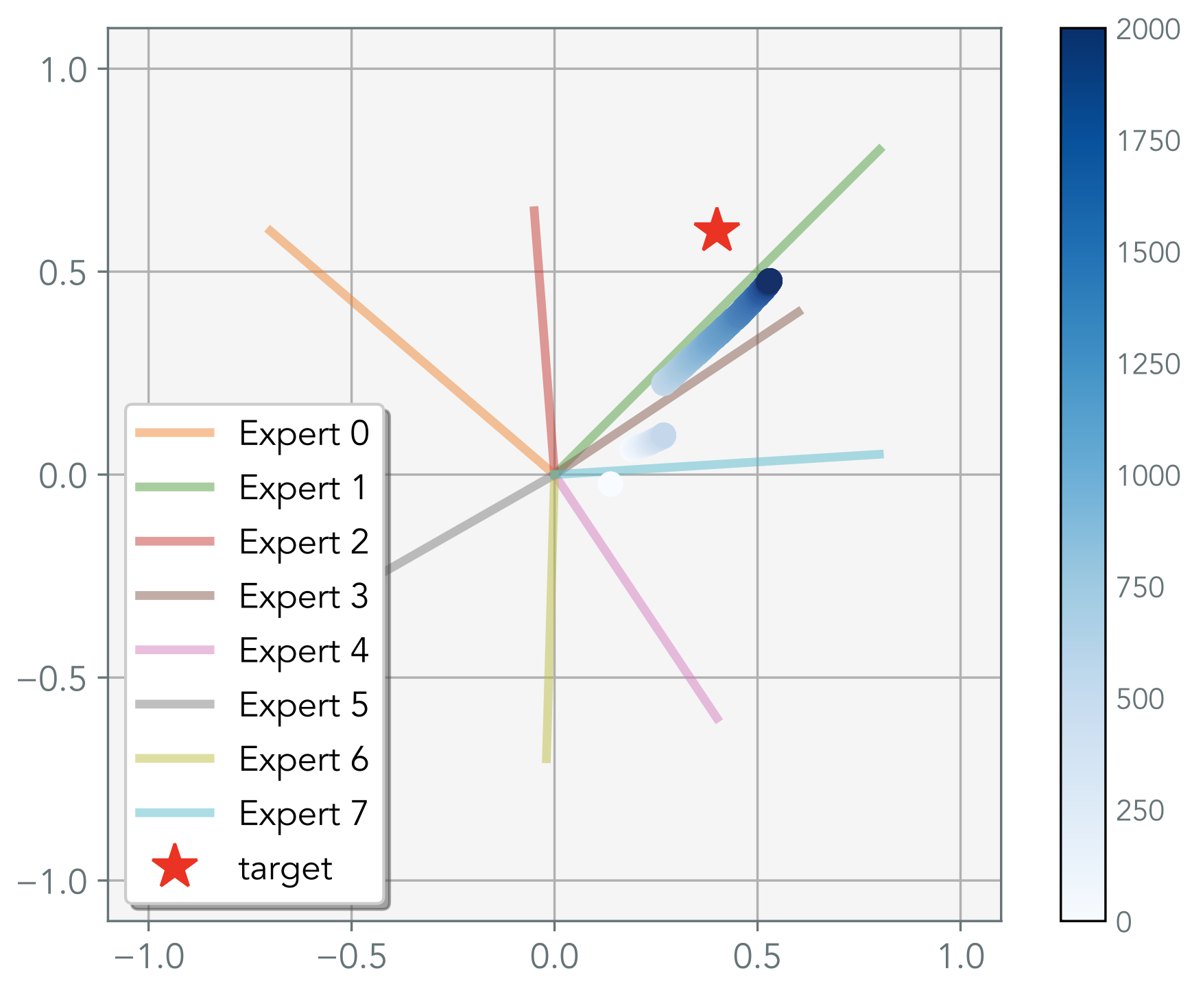
RPO decouples these steps. It selects a subset of experts using one policy, then independently learns how to weight them, solving this issue.

When Routing Doesn’t Matter (But Should)

Interestingly, many MoE models perform well even with poorly trained routers—or even with random routing. Why?

Because the experts themselves adapt. They learn to handle whatever traffic the router sends their way. This means the model is "routing through the experts" rather than through the router.

This is fine during pretraining, but problematic when:

Experts are frozen (e.g., during model stitching),

You want true modularity and reusability.

A Simple 2D Illustration and Toy Experiments

In our toy experiment, we explore a 2D regression problem: each expert is a vector in $\mathbb{R}^2$ , and we want to predict a target vector y. With $k=1$ , standard optimization gets stuck due to interference between similar experts. With $k=2$ , it picks expert pairs that individually minimize loss rather than jointly solve the task. RPO overcomes both issues by explicitly sampling and evaluating expert combinations.

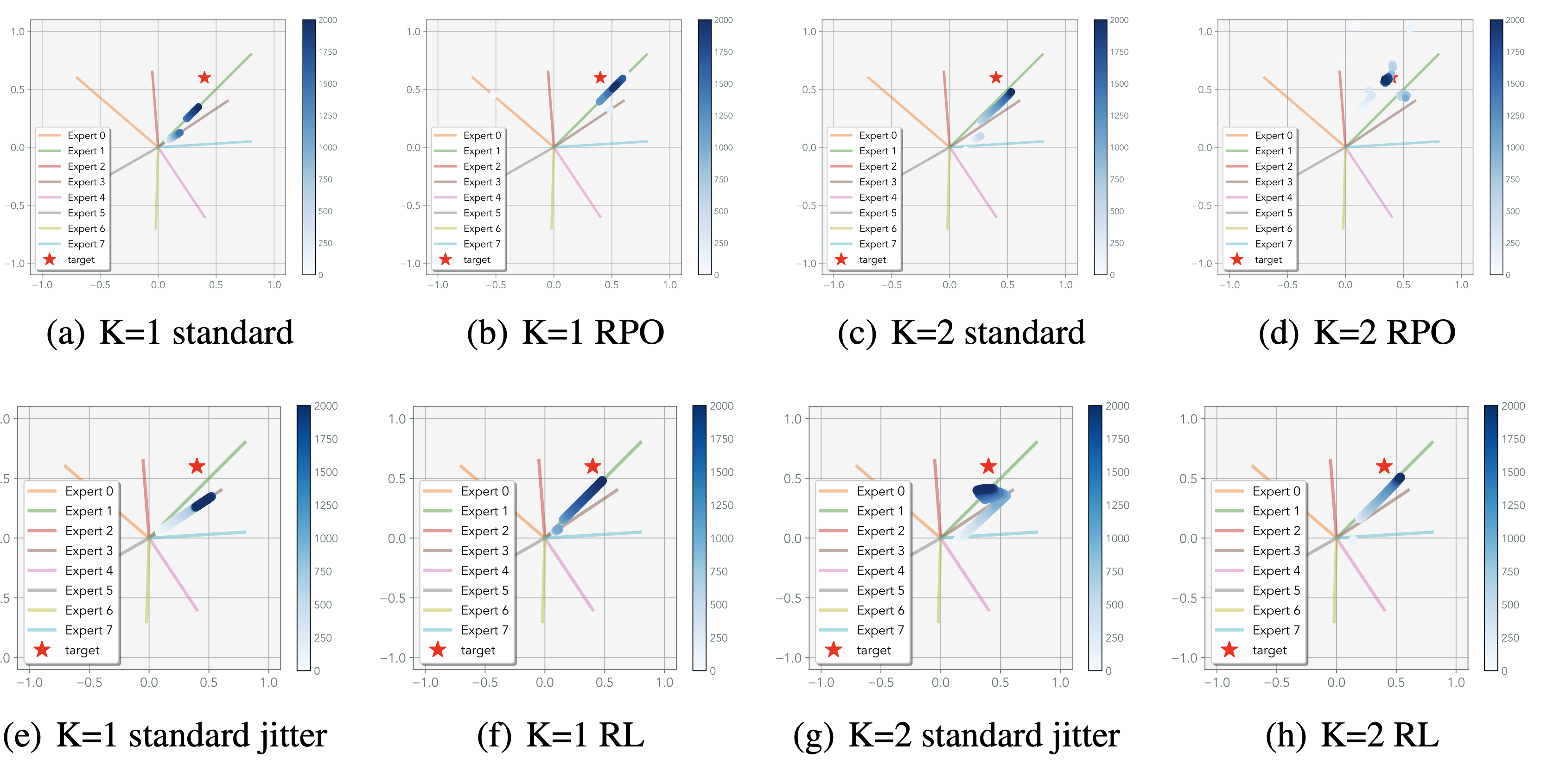
NanoGPT trained on Shakespeare with various MoE configurations.
RPO converges signficantly faster than other methods, due to its ability to quickly commit to a single
expert to solve the task.

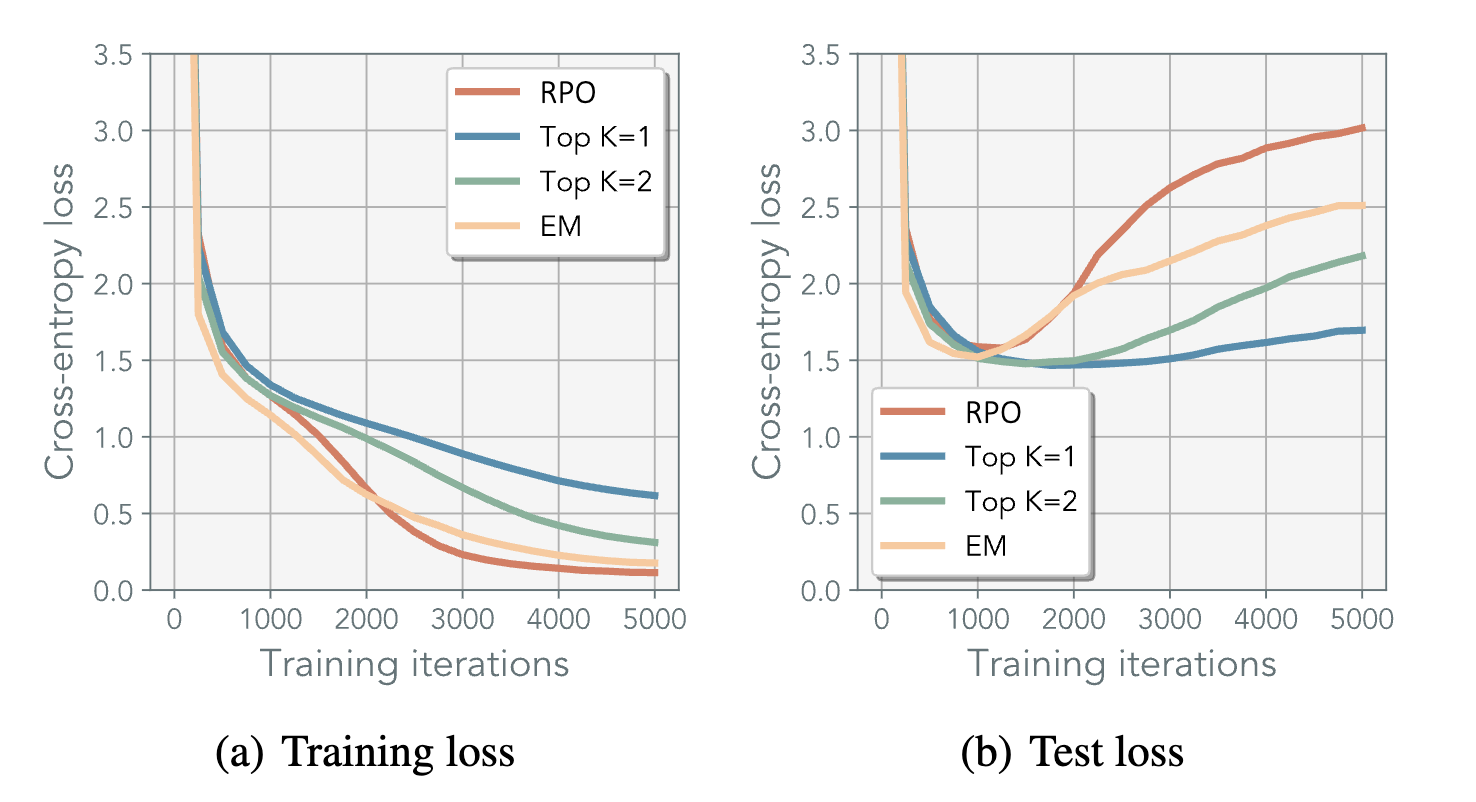
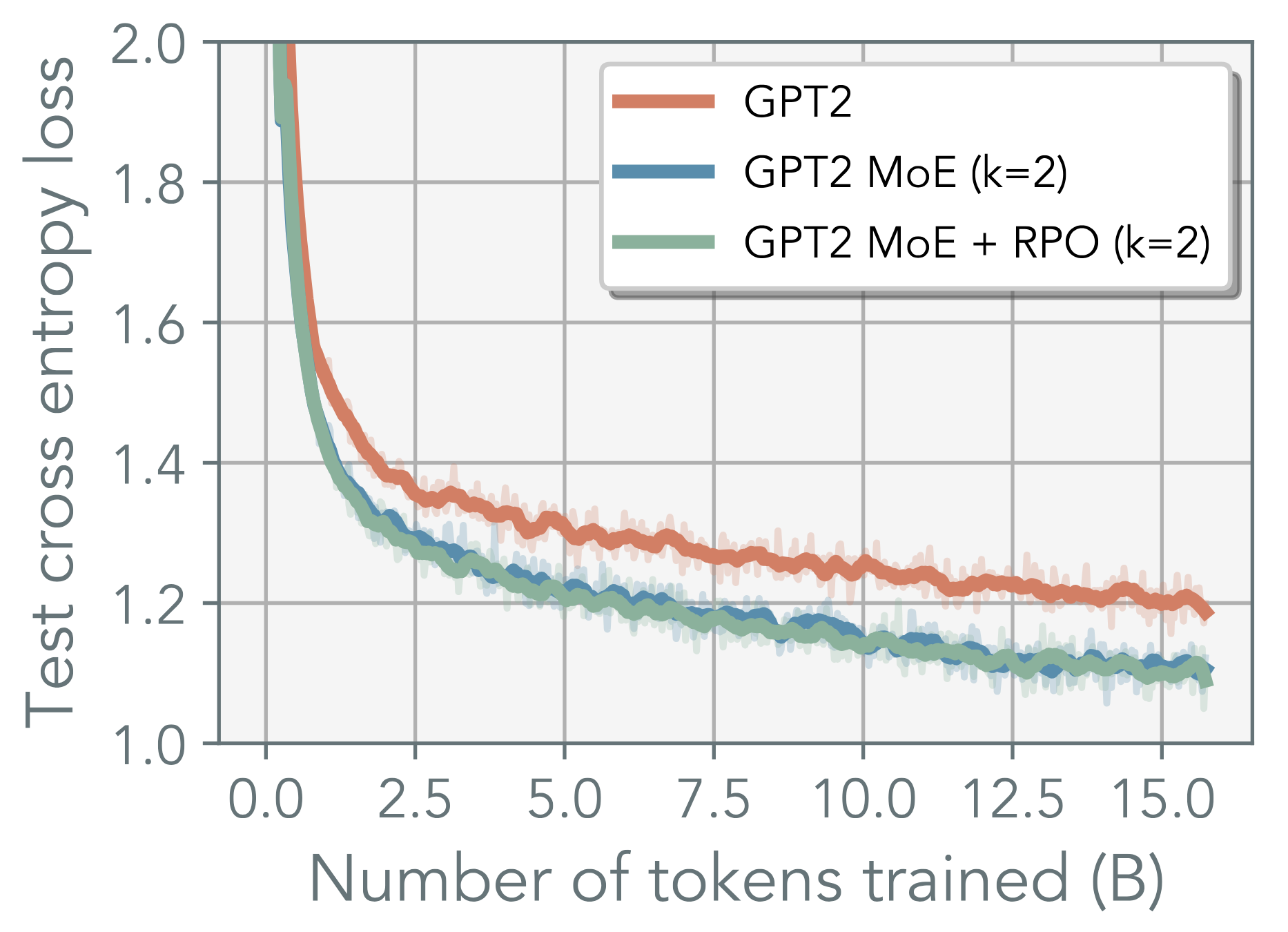
Negative Result

Finally the negative result - RPO doesn’t seem to help on GPT2 training on Tinystories 😞.

Conclusion

This project began as an attempt to make MoEs more adaptive at test time. Along the way, we realized that standard router optimization was poorly aligned with its intended purpose.

Our proposed fix, Router Policy Optimization, didn't scale to full pretraining, but it performed significantly better in model stitching and frozen-expert settings—where correct routing matters most.

As we move toward models that are modular, composable, and reusable, understanding and improving routing optimization will be essential. We hope this post helps you think more critically about how expert selection is trained—and what it should be optimizing.